早教吧作业答案频道 -->数学-->
如图,O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
题目详情
如图, O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交 O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.
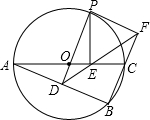
(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)求证:OD=OE;
(3)求证:PF是 O的切线.

(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)求证:OD=OE;
(3)求证:PF是 O的切线.
▼优质解答
答案和解析
(1) ∵AC=12,
∴CO=6,
∴
=
=2π;
答:劣弧PC的长为:2π.
(2)证明:∵PE⊥AC,OD⊥AB,
∠PEA=90°,∠ADO=90°
在△ADO和△PEO中,
,
∴△POE≌△AOD(AAS),
∴OD=EO;
(3)证明:
法一:
如图,连接AP,PC,
∵OA=OP,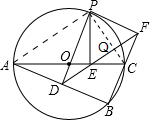
∴∠OAP=∠OPA,
由(2)得OD=EO,
∴∠ODE=∠OED,
又∵∠AOP=∠EOD,
∴∠OPA=∠ODE,
∴AP∥DF,
∵AC是直径,
∴∠APC=90°,
∴∠PQE=90°
∴PC⊥EF,
又∵DP∥BF,
∴∠ODE=∠EFC,
∵∠OED=∠CEF,
∴∠CEF=∠EFC,
∴CE=CF,
∴PC为EF的中垂线,
∴∠EPQ=∠QPF,
∵△CEP∽△CAP
∴∠EPQ=∠EAP,
∴∠QPF=∠EAP,
∴∠QPF=∠OPA,
∵∠OPA+∠OPC=90°,
∴∠QPF+∠OPC=90°,
∴OP⊥PF,
∴PF是 O的切线.
法二:
设 O的半径为r.
∵OD⊥AB,∠ABC=90°,
∴OD∥BF,∴△ODE≌△CFC
又∵OD=OE,∴FC=EC=r-OE=r-OD=r-
BC
∴BF=BC+FC=r+
BC
∵PD=r+OD=r+
BC
∴PD=BF
又∵PD∥BF,且∠DBF=90°,
∴四边形DBFP是矩形
∴∠OPF=90°
OP⊥PF,
∴PF是 O的切线.
∴CO=6,
∴
 |
| PC |
| 60•π•6 |
| 180 |
答:劣弧PC的长为:2π.
(2)证明:∵PE⊥AC,OD⊥AB,
∠PEA=90°,∠ADO=90°
在△ADO和△PEO中,
|
∴△POE≌△AOD(AAS),
∴OD=EO;
(3)证明:
法一:
如图,连接AP,PC,
∵OA=OP,

∴∠OAP=∠OPA,
由(2)得OD=EO,
∴∠ODE=∠OED,
又∵∠AOP=∠EOD,
∴∠OPA=∠ODE,
∴AP∥DF,
∵AC是直径,
∴∠APC=90°,
∴∠PQE=90°
∴PC⊥EF,
又∵DP∥BF,
∴∠ODE=∠EFC,
∵∠OED=∠CEF,
∴∠CEF=∠EFC,
∴CE=CF,
∴PC为EF的中垂线,
∴∠EPQ=∠QPF,
∵△CEP∽△CAP
∴∠EPQ=∠EAP,
∴∠QPF=∠EAP,

∴∠QPF=∠OPA,
∵∠OPA+∠OPC=90°,
∴∠QPF+∠OPC=90°,
∴OP⊥PF,
∴PF是 O的切线.
法二:
设 O的半径为r.
∵OD⊥AB,∠ABC=90°,
∴OD∥BF,∴△ODE≌△CFC
又∵OD=OE,∴FC=EC=r-OE=r-OD=r-
| 1 |
| 2 |
∴BF=BC+FC=r+
| 1 |
| 2 |
∵PD=r+OD=r+
| 1 |
| 2 |
∴PD=BF
又∵PD∥BF,且∠DBF=90°,
∴四边形DBFP是矩形
∴∠OPF=90°
OP⊥PF,
∴PF是 O的切线.
看了 如图,O是△ABC的外接圆,...的网友还看了以下:
已知火车站托运行李的费用C和托运行李的重量P(千克)(P为整数)的对应关系如下表,则C与P的对应关 2020-04-07 …
计算题(P/A,10%,4)=3.1699(P/F,10%,1)=0.9091(P/A,10%,5 2020-04-07 …
A.F,H,C,D,P,A,M,Q,R,S,Y,XB.P,A,C,S,Q,D,F,X,R,H,M,Y 2020-05-26 …
某商品供给量Q对价格P的函数关系为Q=Q(P)=a+b*c的p次方(c≠1)已知当P=2时,Q=3 2020-06-07 …
设一组初始记录关键字序列为(Q,H,C,Y,P,A,M,S,R,D,F,X),则按字母升序的第一趟 2020-07-17 …
设如果当事件A与B同时发生时,事件C必发生,则有(A)P(C)≤P(A)+P(B)-1(B)P(C) 2020-11-05 …
已知abc两两相互独立,求证P(a交b交c)=p(a)p(b)p(c)已知ab相互独立,求证a已知a 2020-12-01 …
下列四个命题:①对立事件一定是互斥事件;②若A,B为两个事件,则P(A∪B)=P(A)+P(B);③ 2020-12-01 …
求助一道概率论的题已知P(A)=1/2,P(B)=1/3,P(C)=1/5,P(AB)=1/10,P 2020-12-13 …
假设事件A和B满足P(BIA)=1则:a:A包含于Bb;A是必然事件c:P(A-B)=0是不是a和c 2021-01-01 …