我们把能够平分一个图形面积的直线叫“好线”，如图1．问题情境：如图2，M是圆O内的一定点，请在图2中作出两条“好线”（要求其中一条“好线”必须过点M），使它们将圆O的面积四等分

Question

我们把能够平分一个图形面积的直线叫“好线”，如图1．

问题情境：如图2，M是圆O内的一定点，请在图2中作出两条“好线”（要求其中一条“好线”必须过点M），使它们将圆O的面积四等分．
小明的思路是：如图3，过点M、O画一条“好线”，过O作OM的垂线，即为另一条“好线”．所以这两条“好线”将的圆O的面积四等分．
问题迁移：
（1）请在图4中作出两条“好线”，使它们将▱ABCD的面积四等分；
（2）如图5，M是正方形ABCD内一定点，请在图5中作出两条“好线”（要求其中一条“好线”必须过点M），使它们将正方形ABCD的面积四等分；
（3）如图6，在四边形ABCD中，AB∥CD，AB+CD=BC，点P是AD的中点，点Q是边BC一点，请作出“好线”PQ将四边形ABCD的面积分成相等的两部分．

Answer 1

（1）如图4，直线AC，BD将▱ABCD的面积四等分，

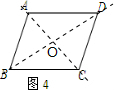
理由如下：
∵四边形ABCD是平行四边形，直线AC，BD是对角线所在的直线，
∴AO=CO，BO=DO，
∴S_△AOB=S_△BOC=S_△OCD=S_△AOD，
∴AC，BD将▱ABCD的面积四等分，
（2）如图5，连接AC、BD相交于点O，作直线OM分别交AD、BC于P、Q两点，过点O作用OM的垂线分别交AB、CD于E、F两点，则直线OM、EF将正方形ABCD的面积四等分．

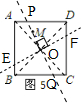
理由如下：
∵点O是正方形ABCD对角线的交点，
∴点O是正方形ABCD的对称中心．
∴AP=CQ，EB=DF．
在△AOP和△EOB中，
∵∠AOP=90°-∠AOE，∠BOE=90°-∠AOE，
∴∠AOP=∠BOE．
∵OA=OB，∠OAP=∠EBO=45°，
∴△AOP≌△EOB（ASA）．
∴AP=BE=DF=CQ．
∴AE=BQ=CF=PD．
设点O到正方形ABCD一边的距离为d，．
∴(1)/(2)（AP+AE）d=(1)/(2)（BE+BQ）d=(1)/(2)（CQ+CF）d=(1)/(2)（DF+PD）d．
∴S_{四边形APOE}=S_{四边形BEOQ}=F_{四边形CQOF}=S_{四边形DFOP}．
∴直线EF、PQ将正方形ABCD面积四等分．
（3）存在．当BQ=CD=时，PQ将四边形ABCD面积二等分．
理由如下：
如图6，延长BA至点E，使AE=CD，延长CD至点F，使DF=AB，连接EF．

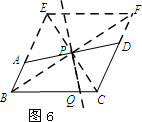
∵BE∥CF，BE=CF．
∴四边形BCFE为平行四边形．
∵BC=BE=AB+CD，
∴平行四边形CBFE为菱形．
连接BF交AD于点M，则△MAB≌△MDF．
∴AM=DM，即点P、M重合．
∴点P是菱形EBCF对角线的交点．
在BC上截取BQ=CD，则CQ=AB．
设点P到菱形EBCF一边的距离为d，
∴S_△ABP+S_△QBP=(1)/(2)（AB+BQ）d=(1)/(2)（CQ+CD）d=S_△CQP+S_△CDP．
∴当BQ=CD时，直线PQ将四边形ABCD的面积分成相等的两部分．