早教吧作业答案频道 -->数学-->
如图,在棱长为1的正方体中,P是侧棱CC1上的一点,CP=m(1)试确定m,使直线AP与平面BDD1B1所成角的正切值为42;(2)在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q在平面APD1上的射影
题目详情
如图,在棱长为1的正方体中,P是侧棱CC1上的一点,CP=m
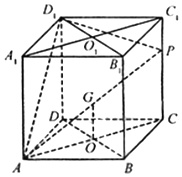
(1)试确定m,使直线AP与平面BDD1B1所成角的正切值为4
;
(2)在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q在平面APD1上的射影垂直于AP,并证明你的结论.

(1)试确定m,使直线AP与平面BDD1B1所成角的正切值为4
| 2 |
(2)在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q在平面APD1上的射影垂直于AP,并证明你的结论.
▼优质解答
答案和解析
(1)连AC,设AC与BD相交于点O,AP与平面BDD1B1相交于点G,
连接OG,因为PC∥平面BDD1B1,平面BDD1B1∩平面APC=OG,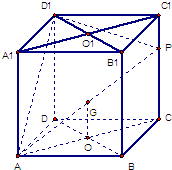
故OG∥PC,所以,OG=
PC=
.
又AO⊥BD,AO⊥BB1,所以AO⊥平面BDD1B1,
故∠AGO是AP与平面BDD1B1所成的角.
在Rt△AOG中,tan∠AGO=
=4
,即m=
.
所以,当m=
时,直线AP与平面BDD1B1所成的角的正切值为4
.
(2)可以推测,点Q应当是AICI的中点,当是中点时
因为D1O1⊥A1C1,且 D1O1⊥A1A,A1C1∩A1A=A1,
所以 D1O1⊥平面ACC1A1,
又AP⊂平面ACC1A1,故 D1O1⊥AP.
那么根据三垂线定理知,D1O1在平面APD1的射影与AP垂直.
连接OG,因为PC∥平面BDD1B1,平面BDD1B1∩平面APC=OG,

故OG∥PC,所以,OG=
| 1 |
| 2 |
| m |
| 2 |
又AO⊥BD,AO⊥BB1,所以AO⊥平面BDD1B1,
故∠AGO是AP与平面BDD1B1所成的角.
在Rt△AOG中,tan∠AGO=
| ||||
|
| 2 |
| 1 |
| 4 |
所以,当m=
| 1 |
| 4 |
| 2 |
(2)可以推测,点Q应当是AICI的中点,当是中点时
因为D1O1⊥A1C1,且 D1O1⊥A1A,A1C1∩A1A=A1,
所以 D1O1⊥平面ACC1A1,
又AP⊂平面ACC1A1,故 D1O1⊥AP.
那么根据三垂线定理知,D1O1在平面APD1的射影与AP垂直.
看了 如图,在棱长为1的正方体中,...的网友还看了以下:
对于非空实数集A,记A*=(yI所有的x属于A,都有y大于等于x).设非空是实数集M,P满足M为P 2020-05-16 …
求助:证明对任意素数p,存在正整数前n项和Sn及前m项和Sm(n,m为正整数),p=Sn/Sm证明 2020-05-17 …
已知m,n,p,q满足:mnpq=6(m-1)(n-1)(p-1)(q-1).(1).若m,n,p 2020-06-11 …
(1/2)已知P:函数y=x^2+mx+1在(-1,正无穷)上单调递增,q:函数y=4x^2+4( 2020-07-13 …
麻烦提供一下具体思路.已知直线L过点P(2,0),斜率为4/3,直线L和抛麻烦提供一下具体思路.已 2020-07-13 …
已知a^3+2a=-2,求3a^6+12a^6-a^3+12a^2-2a-4的值是3a^6+12a 2020-07-22 …
填介词或副词1.Themeetingended6.p.m.选择1.Therearealotofstu 2020-10-30 …
几何分布无记忆性证明中证:P{x=m+n|x>m}=P(X=m+n,x>m)/P{x>m}=P(X= 2020-10-31 …
1、已知:a、b互为相反数,x、y互为倒数,|m|=1,求m的平方-2(a+b+xy)+(a+b)的 2020-11-03 …
已知数列{an}的前n项和Sn满足(p-1)Sn=p²-an(p>0,p≠1)且a3=1\3(1)求 2020-11-04 …