早教吧作业答案频道 -->数学-->
已知△ABC中,BC=2,G为△ABC的重心,且满足AG⊥BG,则△ABC的面积的最大值为.
题目详情
已知△ABC中,BC=2,G为△ABC的重心,且满足AG⊥BG,则△ABC 的面积的最大值为___.
▼优质解答
答案和解析
 设AB中点为O,连接AO,可得重心G在CO上且
设AB中点为O,连接AO,可得重心G在CO上且
=
,
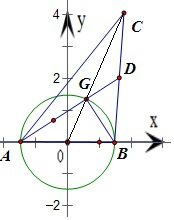
以AB所在直线为x轴,AB中点为原点建立如图所示直角坐标系,
设AB=2r(r>0),则A(-r,0),B(r,0),
设C(x,y),可得G(
,
)
∵AG⊥BG,
∴点G在以AB为直径的圆上运动(A、B两点除外)
由此可得(
)2+(
)2=r2,整理得x2+y2=9r2,
因此,点C在以原点为圆心,半径为3r的圆上运动(x轴上两点除外),
可得,当x=0时,y取得最大值3r,
∴此时,tan
=
,AC=BC=2,
∵r2+(3r)2=2,解得:r=
,
∴此时,S△ABC=
×2r×3r=
.
故答案为:
.
 设AB中点为O,连接AO,可得重心G在CO上且
设AB中点为O,连接AO,可得重心G在CO上且| OG |
| 1 |
| 3 |
| OC |
以AB所在直线为x轴,AB中点为原点建立如图所示直角坐标系,
设AB=2r(r>0),则A(-r,0),B(r,0),
设C(x,y),可得G(
| x |
| 3 |
| y |
| 3 |
∵AG⊥BG,
∴点G在以AB为直径的圆上运动(A、B两点除外)
由此可得(
| x |
| 3 |
| y |
| 3 |
因此,点C在以原点为圆心,半径为3r的圆上运动(x轴上两点除外),
可得,当x=0时,y取得最大值3r,
∴此时,tan
| C |
| 2 |
| 1 |
| 3 |
∵r2+(3r)2=2,解得:r=
| ||
| 5 |
∴此时,S△ABC=
| 1 |
| 2 |
| 6 |
| 5 |
故答案为:
| 6 |
| 5 |
看了 已知△ABC中,BC=2,G...的网友还看了以下:
如果梯形的对角互补,最大角是最小角的3倍,上底为a,下底为b(b>a),则两底间的距离为A:a+b 2020-04-26 …
(1)已知abc属于正实数,求证(a^2+a+1)(b^2+b+1)(c^2+c+1)>=27ab 2020-04-27 …
定义集合A*B={x|x∈A且x不属于B},若A={1,3,5,7},B={2,3,5},则: ( 2020-05-15 …
1、已知a,b,c互不相等求2a-b-c/(a-b)(b-c)+2b-c-a/(b-c)(b-a) 2020-05-16 …
1.[a/(ab-b²)-b/(a²-ab)]÷[1+(a²+b²)/2ab],其中a=-1+根号 2020-05-16 …
计算:(a/a^3+a^b+ab^2+b^3)(b/a^3-a^2b+ab^2-b^3)+(1/a 2020-07-21 …
二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:①4a+c<0;②m(am+b)+ 2020-07-30 …
利用如图所示几何图形的面积可以表示的公式是[]A.a2-b2=a(a-b)+b(a-b)B.(a- 2020-08-02 …
已知a^2+b^2=5,ab=4求代数式5ab^2(a-b)-3ab(b-a)^2+5a^2b(b- 2020-11-20 …
已知数轴上表示ab两点位置如图所示,试判断下列格式的符号:a+b;a-b;b-a;|a|-ba0b- 2020-12-24 …