早教吧作业答案频道 -->数学-->
如图,点C在以AB为直径的圆O上,PA垂直与圆O所在平面,G为△AOC的垂心.(1)求证:平面OPG⊥平面PAC;(2)若PA=AB=2AC=2,点Q在线段PA上,且PQ=2QA,求三棱锥P-QGC的体积.
题目详情
如图,点C在以AB为直径的圆O上,PA垂直与圆O所在平面,G为△AOC的垂心.
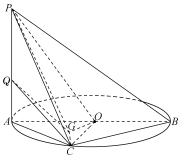
(1)求证:平面OPG⊥平面PAC;
(2)若PA=AB=2AC=2,点Q在线段PA上,且PQ=2QA,求三棱锥P-QGC的体积.

(1)求证:平面OPG⊥平面PAC;
(2)若PA=AB=2AC=2,点Q在线段PA上,且PQ=2QA,求三棱锥P-QGC的体积.
▼优质解答
答案和解析
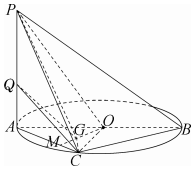 (1)证明:∵G为△AOC的垂心,∴OG⊥AC,
(1)证明:∵G为△AOC的垂心,∴OG⊥AC,
∵PA⊥平面ABC,OG⊂平面ABC,
∴PA⊥OG.
又PA⊂平面PAC,AC⊂平面PAC,PA∩AC=A,
∴OG⊥平面PAC.
又OG⊂平面OPG,
∴平面OPG⊥平面PAC.
(2) 延长OG交AC于点M.
由(1)知OM⊥平面PAC,
即GM为点G到平面PAC的距离.
由已知可得,OA=OC=AC=1,
∴△AOC为正三角形,
∴OM=
.GM=
OM=
.
∵PA=2,PQ=2QA,∴PQ=
.
∴S△PQC=
PQ•CA=
×
×1=
,
∴VP-QGC=VG-PQC=
S△PQC•GM=
×
×
=
.
 (1)证明:∵G为△AOC的垂心,∴OG⊥AC,
(1)证明:∵G为△AOC的垂心,∴OG⊥AC,∵PA⊥平面ABC,OG⊂平面ABC,
∴PA⊥OG.
又PA⊂平面PAC,AC⊂平面PAC,PA∩AC=A,
∴OG⊥平面PAC.
又OG⊂平面OPG,
∴平面OPG⊥平面PAC.
(2) 延长OG交AC于点M.
由(1)知OM⊥平面PAC,
即GM为点G到平面PAC的距离.
由已知可得,OA=OC=AC=1,
∴△AOC为正三角形,
∴OM=
| ||
| 2 |
| 1 |
| 3 |
| ||
| 6 |
∵PA=2,PQ=2QA,∴PQ=
| 4 |
| 3 |
∴S△PQC=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
∴VP-QGC=VG-PQC=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| ||
| 6 |
| ||
| 27 |
看了 如图,点C在以AB为直径的圆...的网友还看了以下:
客户发来一封邮件是这样的:WeneedtohaveyourO/CorP/Iforthisorder 2020-04-27 …
(200小•湖北)在R上定义运算:p⊗q=−o一(p−c)(q−b)+hbc(b、c∈R是常数), 2020-05-13 …
在xy平面,直线L过原点O,和点A,A不等于O.取一点P,过P点做L的垂线和L相交于Q点,如果P点 2020-05-16 …
设有字符序列(Q,H,C,Y,P,A,M,S,R,D,F,x),则新序列(H,C,Q,P,A,M,S 2020-05-23 …
已知3个类O、P和Q,其中,类O由类P的1个实例和类Q的1个或多个实例构成。能够正确表示类O、P和Q 2020-05-26 …
函数y=-3/4x-6的图象分别交x轴 y轴与A C两点1.在X轴上找出点B 使△ACB∽△AOC 2020-06-27 …
若有以下定义和赋值double*q,a=5.5;int*p,i=1;double*q,a=5.5; 2020-07-09 …
设一组初始记录关键字序列为(Q,H,C,Y,P,A,M,S,R,D,F,X),则按字母升序的第一趟 2020-07-17 …
选出下面各项中字音有误的一项:A前仆后继pū风尘仆仆、仆人pú漂飘泊piāoB漂白piǎo漂亮pià 2020-11-07 …
设有定义:intn=0,*p=&n,**q=&p;则下列选项中,正确的赋值语句是A)p=1;B)*q 2020-12-31 …