早教吧作业答案频道 -->数学-->
如图,已知等边△ABC的边长是2cm,将边AC沿射线BC的方向平移2cm,得到线段DE,连接AD、CE.(1)求证:四边形ACED是菱形;(2)将△ABC绕点C旋转,当CA′与DE交于一点M,CB′与AD交于一点N时,
题目详情
如图,已知等边△ABC的边长是2cm,将边AC沿射线BC的方向平移2cm,得到线段DE,连接AD、CE.
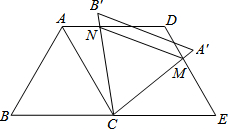
(1)求证:四边形ACED是菱形;
(2)将△ABC绕点C旋转,当CA′与DE交于一点M,CB′与AD交于一点N时,点M、N和点D构成△DMN,试探究△DMN的周长是否存在最小值?如果存在,求出该最小值;如果不存在,请说明理由.

(1)求证:四边形ACED是菱形;
(2)将△ABC绕点C旋转,当CA′与DE交于一点M,CB′与AD交于一点N时,点M、N和点D构成△DMN,试探究△DMN的周长是否存在最小值?如果存在,求出该最小值;如果不存在,请说明理由.
▼优质解答
答案和解析
证明:(1)由平移可得:
∴AD∥CE,AD=CE,
∴四边形ACED是平行四边形,
又∵AD=2cm=AC,
∴□ACED是菱形;
(2)连接CD,
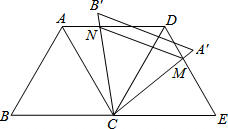
∵∠ACD=∠B'CA'=60°即∠ACN+∠NCD=∠NCD+∠DCA'=60°,
∴∠ACN=∠DCM,
在△ACN和△DCM中,
,
∴△ACN≌△DCM(ASA),
∴AN=DM,
同理,CN=CM,
∵∠NCD+∠DCM=60°,
∴△CMN是等边三角形,
∴MN=CN=CM,
则AN+DN=AD=2.
∴△DMN的周长即为DN+DM+MN=AD+CN,
当CB’⊥AD时,(CN)最小=
,即△DMN的周长的最小值是2+
.
∴AD∥CE,AD=CE,
∴四边形ACED是平行四边形,
又∵AD=2cm=AC,
∴□ACED是菱形;
(2)连接CD,

∵∠ACD=∠B'CA'=60°即∠ACN+∠NCD=∠NCD+∠DCA'=60°,
∴∠ACN=∠DCM,
在△ACN和△DCM中,
|
∴△ACN≌△DCM(ASA),
∴AN=DM,
同理,CN=CM,
∵∠NCD+∠DCM=60°,
∴△CMN是等边三角形,
∴MN=CN=CM,
则AN+DN=AD=2.
∴△DMN的周长即为DN+DM+MN=AD+CN,
当CB’⊥AD时,(CN)最小=
| 3 |
| 3 |
看了 如图,已知等边△ABC的边长...的网友还看了以下:
已知(如图所示)A(3,2),B(3,4),C(-4,-2),D(2,-2),(1)A与B是对称点 2020-05-02 …
已知如图,数轴上A、B、C、D四点对应的有理数分别是整数a、b、c、d,且c-2a=7,则原点应是 2020-05-15 …
已知数轴上A、B两点坐标分别为-3、-6,若在数轴找一点C,使得A与C的距离为4.找一点D,使得B 2020-05-16 …
如图,EC⊥CF于C,点A在CE上,点B在CF上,BD平分∠CBA,AG平分∠EAB,且直线AG交 2020-06-27 …
已知数在线A、B两点坐标分别为-3、-6,若在数在线找一点C,使得A与C的距离为4;找一点D,使得 2020-07-15 …
如图所示,电荷量均为+Q的点电荷A、B连线上有a、c两点,在连线的中垂线上有b、d两点,a、b、c 2020-07-21 …
如图所示,P、Q是矩形ABCD的AD边和BC边的中点,E、F是AB边和CD边的中点,MP=QN,M 2020-08-01 …
读某区域图,图中虚线为运河,回答下列问题。(8分)(1)图中A、B两条河流的流向为:A河,B河。(2 2020-12-08 …
已知数轴上A、B两点坐标分别为-3、-6,若在数轴上找一点C,使得A与C的距离为4;找一点D,使得B 2020-12-14 …
直线y=-3/4x+3与x轴y轴分别交于A,B两点,点C(X,Y)是y=-3/4x+3的动点过点C的 2021-01-10 …