早教吧作业答案频道 -->数学-->
如图,四边形ABCD中,∠BCD是钝角,AB=AD,BD平分∠ABC.若CD=3,BD=26,sin∠DBC=33.(1)求BC的长;(2)求证:△BCD≌△BAD;(3)求对角线AC的长.
题目详情
如图,四边形ABCD中,∠BCD是钝角,AB=AD,BD平分∠ABC.若CD=3,BD=2
,sin∠DBC=
.
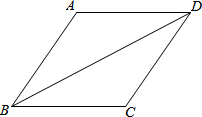
(1)求BC的长;
(2)求证:△BCD≌△BAD;
(3)求对角线AC的长.
| 6 |
| ||
| 3 |

(1)求BC的长;
(2)求证:△BCD≌△BAD;
(3)求对角线AC的长.
▼优质解答
答案和解析
(1)如图,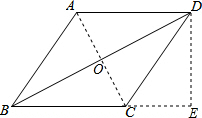 过D作DE⊥BC交BC的延长线于E,
过D作DE⊥BC交BC的延长线于E,
则∠E=90°,
∵sin∠DBC=
,BD=2
,
∴DE=2
,
∵CD=3,
∴CE=1,BE=4,
∴BC=3,
(2)∵BC=3,CD=3
∴BC=CD,
∴∠CBD=∠CDB,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠ABD=∠ADB=∠CBD=∠CDB,
∵BD=BD,
∴△BCD≌△BAD;
(3)由(2)知,∠ABD=∠CDB,
∴AB∥CD,
同理AD∥BC,
∴四边形ABCD是菱形,
连接AC交BD于O,
则AC⊥BD,AO=CO,BO=DO=
,
∴OC=
=
,
∴AC=2
.
 过D作DE⊥BC交BC的延长线于E,
过D作DE⊥BC交BC的延长线于E,则∠E=90°,
∵sin∠DBC=
| ||
| 3 |
| 6 |
∴DE=2
| 2 |
∵CD=3,
∴CE=1,BE=4,
∴BC=3,
(2)∵BC=3,CD=3
∴BC=CD,
∴∠CBD=∠CDB,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠ABD=∠ADB=∠CBD=∠CDB,
∵BD=BD,
∴△BCD≌△BAD;
(3)由(2)知,∠ABD=∠CDB,
∴AB∥CD,
同理AD∥BC,
∴四边形ABCD是菱形,
连接AC交BD于O,
则AC⊥BD,AO=CO,BO=DO=
| 6 |
∴OC=
| BC2-BO2 |
| 3 |
∴AC=2
| 3 |
看了 如图,四边形ABCD中,∠B...的网友还看了以下:
在0.1mol/LNa2S溶液中,下列关系式正确的是()A.c(Na+)>c(OH-)>c(HS- 2020-05-13 …
给下列加粗字选择正确的读音。(填序号)(1)乙醚()A.míB.mǐC.mī(2)犁铧()A.hu 2020-05-14 …
A、B、C、D四个带电的小球,B球吸引A球,B球排斥C球,C球吸引D球,若C球带正电,则当A球和D 2020-06-16 …
A.B.C.D.E.F和G都是有机化合物,它们的关系如下图所示(1)化合物C的分子式是C7H8O, 2020-06-18 …
读图,判断问题。小题1:四国均有典型的放牧业,其中以牧牛业为主的是A.①B.②C.③D.④小题2: 2020-06-20 …
a、b、c表示三个数,则乘法结合律可以用()式子表示.A.(a+b)+c=a+(b+c)B.(a× 2020-07-31 …
已知三条不同的直线a、b、c在同一平面内,下列四条命题:①如果a∥b,a⊥c,那么b⊥c;②如果b 2020-08-01 …
已知三条不同的直线a、b、c在同一平面内,下列四条命题:①如果a∥b,a⊥c,那么b⊥c;②如果b∥ 2020-11-02 …
已知三条不同的直线a,b,c在同一平面内,下列四个命题:①如果a∥b,a⊥c,那么b⊥c;②如果b∥ 2020-11-02 …
下图为某地区港口分布示意图。完成题。1.导致a港口解冻日期比其他港口晚的主要因素是2.b.c.d三港 2020-11-04 …