早教吧作业答案频道 -->数学-->
某植物园要建形状为直角梯形的苗圃(如图所示),两条邻边借用夹角为135°的两面墙,另两条边的总长为60m,设垂直于底边的腰长为x(m).(1)求苗圃面积S关于边长x的函数解析式S(x)
题目详情
某植物园要建形状为直角梯形的苗圃(如图所示),两条邻边借用夹角为135°的两面墙,另两条边的总长为60m,设垂直于底边的腰长为x(m).
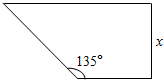
(1)求苗圃面积S关于边长x的函数解析式S(x)并指出该函数的定义域;
(2)当x为何值时,面积S最大?最大面积是多少?

(1)求苗圃面积S关于边长x的函数解析式S(x)并指出该函数的定义域;
(2)当x为何值时,面积S最大?最大面积是多少?
▼优质解答
答案和解析
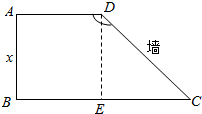 (1)过点D作DE⊥BC于E,则四边形ADBE为矩形,DE=AB=x,∠ADE=∠DEB=90°,
(1)过点D作DE⊥BC于E,则四边形ADBE为矩形,DE=AB=x,∠ADE=∠DEB=90°,
则∠CDE=∠ADC-∠ADE=45°,
在直角△CDE中,
又∵∠DEC=90°,
∴∠C=45°,
∴CE=DE=x,
∵BC=60-AB=60-x,
∴BE=BC-CE=60-2x,
∴AD=BE=60-2x,
∴梯形ABCD面积S=
(AD+BC)•AB=
(60-2x+60-x)•x=-
x2+60x,
∵
,
∴0<x<30.
故梯形ABCD面积S与x之间的函数关系式为S=-
x2+60x(0<x<30);
(2)∵S=-
x2+60x=-
(x-20)2+600
∵0<x<30,
∴x=20m时,S有最大值600m2.
 (1)过点D作DE⊥BC于E,则四边形ADBE为矩形,DE=AB=x,∠ADE=∠DEB=90°,
(1)过点D作DE⊥BC于E,则四边形ADBE为矩形,DE=AB=x,∠ADE=∠DEB=90°,则∠CDE=∠ADC-∠ADE=45°,
在直角△CDE中,
又∵∠DEC=90°,
∴∠C=45°,
∴CE=DE=x,
∵BC=60-AB=60-x,
∴BE=BC-CE=60-2x,
∴AD=BE=60-2x,
∴梯形ABCD面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵
|
∴0<x<30.
故梯形ABCD面积S与x之间的函数关系式为S=-
| 3 |
| 2 |
(2)∵S=-
| 3 |
| 2 |
| 3 |
| 2 |
∵0<x<30,
∴x=20m时,S有最大值600m2.
看了 某植物园要建形状为直角梯形的...的网友还看了以下:
急急急、还有分加.1-2+3-4+5-6+…+87-88=?长方形的一边长等于3a+2b,另一边比 2020-06-23 …
一个四边形的周长是46cm,已知第一条边长是acm,第二条边长比第一条边长的三倍还少5cm,第三条 2020-07-17 …
相邻两边长的比值是黄金比的矩形,叫做黄金矩形,从外形看,它最具美感.现在想要制作一张“黄金矩形”的 2020-07-28 …
1用火柴棒拼出两个边长等于棒长的等边三角形,你要几种拼法,最少需要几根火柴棒?2拼6个边长等于等边 2020-08-01 …
一个四边形的周长是48CM,已知第一条边长是A,第二条边比第一条边的2倍长3CM,第三条边长等于第一 2020-11-24 …
四边形的判定一个四边形的周长是48cm,已知第一条边长是acm,第二条边比第一条边的2倍长3cm,第 2020-11-24 …
一个四边形的周长是24cm,已知第一条边长是acm,第二条边比第一条边的2倍少3cm,第三条边长等于 2020-11-24 …
七年级数学(上)复习题二11题一个四边形的周长是48cm,已知第一条边长是acm,第二条边比第一条边 2020-11-24 …
用火柴棒拼搭等边三角形(1)用火柴棒拼搭出两个边长等于棒长的等边三角形,你有几种拼法,最少需要几根火 2020-11-24 …
一个环形,它外圆半径等于一个正方形边长,从这个正方形取一个边长是内圆半径的正方有一个环形,它的外圆半 2021-01-16 …