早教吧作业答案频道 -->数学-->
如图,在菱形ABCD中,∠A=60°,点E,F分别是边AB,AD上的点,且满足∠BCE=∠DCF,连结EF.(1)若AF=1,求EF的长;(2)取CE的中点M,连结BM,FM,BF.求证:BM⊥FM.
题目详情
如图,在菱形ABCD中,∠A=60°,点E,F分别是边AB,AD上的点,且满足∠BCE=∠DCF,连结EF.
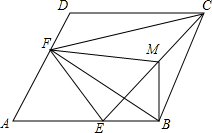
(1)若AF=1,求EF的长;
(2)取CE的中点M,连结BM,FM,BF.求证:BM⊥FM.

(1)若AF=1,求EF的长;
(2)取CE的中点M,连结BM,FM,BF.求证:BM⊥FM.
▼优质解答
答案和解析
(1) ∵四边形ABCD是菱形,
∴AB=AD=BC=DC,∠D=∠CBE,
又∵∠BCE=∠DCF,
在△CBE与△CDF中,
,
∴△CBE≌△CDF,
∴BE=DF.
又∵AB=AD,
∴AB-BE=AD-DF,即AE=AF,
又∵∠A=60°,
∴△AEF是等边三角形,
∴EF=AF,
∵AF=1,
∴EF=1.
(2)证明:如图1,延长BM交DC于点N,连结FN,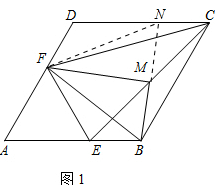
∵四边形ABCD是菱形,
∴DC∥AB,
∴∠NCM=∠BEM,∠CNM=∠EBM
∵点M是CE的中点,
∴CM=EM.
在△CMN与△EMB中,
,
∴△CMN≌△EMB,
∴NM=MB,CN=BE.
又∵AB=DC.
∴DC-CN=AB-BE,即DN=AE.
∵△AEF是等边三角形,
∴∠AEF=60°,EF=AE.
∴∠BEF=120°,EF=DN.
∵DC∥AB,
∴∠A+∠D=180°,
又∵∠A=60°,
∴∠D=120°,
∴∠D=∠BEF.
在△FDN与△BEF中,
,
∴△FDN≌△BEF,
∴FN=FB,
又∵NM=MB,
∴BM⊥MF
∴AB=AD=BC=DC,∠D=∠CBE,
又∵∠BCE=∠DCF,
在△CBE与△CDF中,
|
∴△CBE≌△CDF,
∴BE=DF.
又∵AB=AD,
∴AB-BE=AD-DF,即AE=AF,
又∵∠A=60°,
∴△AEF是等边三角形,
∴EF=AF,
∵AF=1,
∴EF=1.
(2)证明:如图1,延长BM交DC于点N,连结FN,

∵四边形ABCD是菱形,
∴DC∥AB,
∴∠NCM=∠BEM,∠CNM=∠EBM
∵点M是CE的中点,
∴CM=EM.
在△CMN与△EMB中,
|
∴△CMN≌△EMB,
∴NM=MB,CN=BE.
又∵AB=DC.
∴DC-CN=AB-BE,即DN=AE.
∵△AEF是等边三角形,
∴∠AEF=60°,EF=AE.
∴∠BEF=120°,EF=DN.
∵DC∥AB,
∴∠A+∠D=180°,
又∵∠A=60°,
∴∠D=120°,
∴∠D=∠BEF.
在△FDN与△BEF中,
|
∴△FDN≌△BEF,
∴FN=FB,
又∵NM=MB,
∴BM⊥MF
看了 如图,在菱形ABCD中,∠A...的网友还看了以下:
图a、图b是两种声音的波形,从图可知:图a是的波形,理由是;图b是的. 2020-05-02 …
DNA分子能准确无误地进行复制的原因是()A.碱基之间由氢键相连B.DNA的半保留复制C.DNA的 2020-05-14 …
请问这个烃怎么命名?CH3 - CH2 - CH – CH - CH2 - CH3| |CH3 C 2020-05-16 …
把下列句子组合成语意连贯的一段话。(只填序号)A.读过《红楼梦》的人,自能体会诗中悲凉的意味。B. 2020-05-17 …
英语翻译英语翻译一下:A:你卧室里有一张床吗?B:是的,有.A:床上有什么东西?B:有一张床单,一 2020-05-24 …
构造4阶方阵A,B是的矩阵A,B,A+B都是正交矩阵.如果是奇数阶方阵,还能构造嘛?A,B均为正定 2020-06-04 …
有一条题如下:会建造房屋,开始过定居生活的居民是A.大汶口原始居民B.河姆渡和半坡原始居民我想问的 2020-06-06 …
英语翻译A伙计.你喜欢NBA吗?B是的,当然了!我可是个忠实的热火球迷呢、A我也喜欢NBA,你的偶 2020-07-27 …
英语翻译应该不难吧?翻译英文:A:你是姚明吗?B:是的,我是.A:姚明你为什么喜欢篮球?B:因为它可 2020-10-30 …
若a,b是异面直线,则只需具备的条件是()A.a⊂平面α,b⊄平面α,a与b不平行B.a⊂平面α,b 2020-11-02 …