如图一，菱形ABCD的边长为2，点E是AB的中点，且DE⊥AB．（1）求证：△ABD是等边三角形；（2）将图一中△ADE绕点D逆时针旋转，使得点

Question

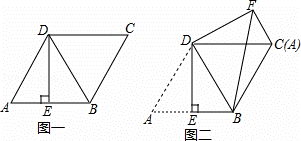
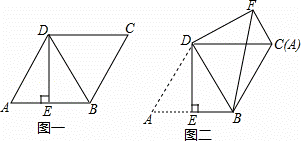
如图一，菱形 ABCD 的边长为 2 ，点 E 是 AB 的中点，且 DE ⊥ AB ．

（ 1 ）求证： △ ABD 是等边三角形；

（ 2 ）将图一中 △ ADE 绕点 D 逆时针旋转，使得点 A 和点 C 重合，得到 △ CDF ，连接 BF ，如图二，求线段 BF 的长．

Answer 1

       （ 1 ）证明：如图一，

∵ 点 E 是 AB 的中点，且 DE ⊥ AB ，

∴ AD=BD ，

∵ 四边形 ABCD 是菱形，

∴ AD=AB ，

∴ AD=DB=AB ，

∴△ ABD 是等边三角形；

（ 2 ）如图二，

由（ 1 ）得： △ ABD 是等边三角形，

则 ∠ ADE= ∠ BDE ，

∵ 四边形 ABCD 是菱形，

∴ AB ∥ DC ，

∵ DE ⊥ AB ，

∴∠ EDC=90 ° ，

∴∠ BDF= ∠ FDC+ ∠ CDB= ∠ EDB+ ∠ CDB=90 ° ，

∵△ ADE 绕点 D 逆时针旋转，使得点 A 和点 C 重合，得到 △ CDF ，

∴ DF=ED= ， BD=2 ，

∴ BF= ．