早教吧作业答案频道 -->数学-->
△ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A按顺时针旋转α得到△AEF,连接BE,CF,它们交于D点,①求证:BE=CF.②当α=120°,求∠FCB的度数.③当四边形ACDE是菱形时,求BD的长.
题目详情
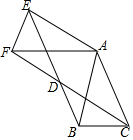
△ABC中,AB=AC=1,∠BAC=45°,将△ABC绕点A按顺时针旋转α得到△AEF,连接BE,CF,它们交于D点,
①求证:BE=CF.
②当α=120°,求∠FCB的度数.
③当四边形ACDE是菱形时,求BD的长.
①求证:BE=CF.
②当α=120°,求∠FCB的度数.
③当四边形ACDE是菱形时,求BD的长.

▼优质解答
答案和解析
①证明:∵△ABC绕点A按顺时针方向旋转角α得到△AEF,
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴AB=AC=AE=AF,
∠EAF+∠FAB=∠BAC+∠FAB,即∠EAB=∠FAC,
在△AEB和△AFC中,
,
∴△AEB≌△AFC,
∴BE=CF;
② ∵α=120°,
∴∠FAC=120°,
而AF=AC,
∴∠ACF=30°,
∵AB=AC,∠BAC=45°,
∴∠ACB=67.5°,
∴∠BCF=67.5°-30°=37.5°;
③ ∵四边形ACDE是菱形,
∴AC∥DE,DE=AE=AC=1,
∴∠ABE=∠BAC=45°,
而AE=AB,
∴△ABE为等腰直角三角形,
∴BE=
AB=
,
∴BD=BE-DE=
-1.
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴AB=AC=AE=AF,
∠EAF+∠FAB=∠BAC+∠FAB,即∠EAB=∠FAC,

在△AEB和△AFC中,
|
∴△AEB≌△AFC,
∴BE=CF;
② ∵α=120°,
∴∠FAC=120°,
而AF=AC,
∴∠ACF=30°,
∵AB=AC,∠BAC=45°,
∴∠ACB=67.5°,
∴∠BCF=67.5°-30°=37.5°;
③ ∵四边形ACDE是菱形,
∴AC∥DE,DE=AE=AC=1,
∴∠ABE=∠BAC=45°,
而AE=AB,
∴△ABE为等腰直角三角形,
∴BE=
| 2 |
| 2 |
∴BD=BE-DE=
| 2 |
看了 △ABC中,AB=AC=1,...的网友还看了以下:
double (*A)[3] =new double[3][3] 怎么样转换成C语句之前已经定义o 2020-05-14 …
矩阵旋转题目矩阵M=(根号200根号2),绕原点逆时针旋转派/4的变化所对应矩阵为N.求矩阵N(2 2020-05-17 …
已知在△ABC中,∠C=90°,AC=3,BC=4.在平面内将△ABC绕B点旋转,点A落到A′,点 2020-07-04 …
有大、中、小3个齿轮互相咬合在一起,若A转动8圈时,B转动5圈,B转动6圈时带动C转动4圈.当A转 2020-07-08 …
从聊城市天气预报图中,不能获取的信息是()A.白天到夜间晴转多云B.南风4-5级转3-4级C.白天最 2020-11-13 …
读图是滨州某日的天气预报图,据图回答4-6题图中天气符号表达的天气状况的是()A.小雨转多云B.中雨 2020-11-13 …
四冲程内燃机在一个工作循环中()A.活塞往复运动2次,曲轴转动2周,完成四个冲程,对外做1次功B.活 2021-01-14 …
四冲程内燃机在一个工作循环中()A.活塞往复运动2次,曲轴转动2周,完成四个冲程,对外做1次功B.活 2021-01-14 …
四冲程内燃机在f个工作循环中()A.活塞往复运动2次,曲轴转动2周,完成四个冲程,对外做1次功B.活 2021-01-14 …
ABCD是四种化学物质,A是固体单质,气体C常用来灭火,D是常见的建筑材料,(“>”表示物质间的转化 2021-01-19 …