早教吧作业答案频道 -->数学-->
如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.(1)求证:四边形ACBP是菱形;(2)若⊙O半径为1,求菱形ACBP的面积.
题目详情
如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.
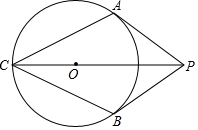
(1)求证:四边形ACBP是菱形;
(2)若⊙O半径为1,求菱形ACBP的面积.

(1)求证:四边形ACBP是菱形;
(2)若⊙O半径为1,求菱形ACBP的面积.
▼优质解答
答案和解析
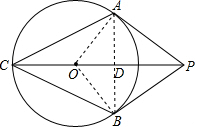 (1)连接AO,BO,
(1)连接AO,BO,
∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO=
∠APB=30°,
∴∠AOP=60°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠AOP=∠CAO+∠ACO,
∴∠ACO=30°,
∴∠ACO=∠APO,
∴AC=AP,
同理BC=PB,
∴AC=BC=BP=AP,
∴四边形ACBP是菱形;
(2)连接AB交PC于D,
∴AD⊥PC,
∴OA=1,∠AOP=60°,
∴AD=
OA=
,
∴PD=
,
∴PC=3,AB=
,
∴菱形ACBP的面积=
AB•PC=
.
 (1)连接AO,BO,
(1)连接AO,BO,∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO=
| 1 |
| 2 |
∴∠AOP=60°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠AOP=∠CAO+∠ACO,
∴∠ACO=30°,
∴∠ACO=∠APO,
∴AC=AP,
同理BC=PB,
∴AC=BC=BP=AP,
∴四边形ACBP是菱形;
(2)连接AB交PC于D,
∴AD⊥PC,
∴OA=1,∠AOP=60°,
∴AD=
| ||
| 2 |
| ||
| 2 |
∴PD=
| 3 |
| 2 |
∴PC=3,AB=
| 3 |
∴菱形ACBP的面积=
| 1 |
| 2 |
3
| ||
| 2 |
看了 如图,PA、PB是⊙O的切线...的网友还看了以下:
已知A=2X方+7X-1,B=4X+1.分别求出满足下列条件的X的值.1.A与B的值互为相反数.2 2020-04-27 …
关于空间解析几何.1.设向量a,b,c两两垂直,且a的模为1,b的模为2,c的模为3,计算a+b+ 2020-05-14 …
要比较1+a与1-a的大小,首先要比较a与-a的大小而a与-a的大小由a的符号确定,故应分类讨论当 2020-06-25 …
要比较1+a与1-a的大小,首先要比较a与-a的大小,而a与-a的大小由a的符号决定,故作分类讨论 2020-06-25 …
比较1+a与1-a的大小,首先要比较a与-a的大小而a与-a的大小由a的正负确定(1)当a>0时, 2020-07-09 …
a>b时1/a与1/b的大小关系a>b时1/a与1/b的大小关系 2020-07-18 …
关于向量代数的几个小题(写出过程)1.设向量a的模=√3,b的模=1,a与b的夹角是π/6,求向量a 2020-11-06 …
概率论与数理统计题问题,设事件A与B的概率分别为1/3与1/2求在下列三种情况下P(BA)的值1.A 2020-12-01 …
1、已知a>b>0,比较1/a与1/b的大小.2、下列命题中正确的是:()A、如果ac>bc,则a> 2021-01-04 …
高中不等式部分1已知a≥1,比较M=√(a+1)-√a与N=√a-√(a-1)的大小做差,做商,都没 2021-01-22 …