早教吧作业答案频道 -->数学-->
如图,四边形ABCD为矩形,E为BC边中点,以AD为直径的O与AE交于点F.(1)求证:四边形AOCE为平行四边形;(2)求证:CF与O相切;(3)若F为AE的中点,求∠ADF的大小.
题目详情
如图,四边形ABCD为矩形,E为BC边中点,以AD为直径的 O与AE交于点F.

(1)求证:四边形AOCE为平行四边形;
(2)求证:CF与 O相切;
(3)若F为AE的中点,求∠ADF的大小.

(1)求证:四边形AOCE为平行四边形;
(2)求证:CF与 O相切;
(3)若F为AE的中点,求∠ADF的大小.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠ADC=90°,
∵E为BC边中点,AO=DO,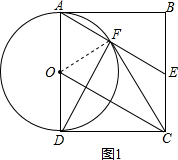
∴AO=
AD,EC=
BC,
∴AO=EC,AO∥EC,
∴四边形OAEC是平行四边形;
(2)如图1,连接OF,
∵四边形OAEC是平行四边形
∴AE∥OC,
∴∠DOC=∠OAF,
∠FOC=∠OFA,
∵OA=OF,
∴∠OAF=∠OFA,
∴∠DOC=∠FOC,
在△ODC与△OFC中,
,
∴△ODC≌△OFC(SAS),
∴∠OFC=∠ODC=90°,
∴OF⊥CF,
∴CF与 O相切;
(3)如图2,连接DE,
∵AD是直径,
∴∠AFD=90°,
∵点F为AE的中点,
∴DF为AE的垂直平分线,
∴DE=AD,
在△ABE与R△DCE中,
,
∴△ABE≌△DCE,
∴AE=DE,
∴AE=DE=AD,
∴三角形ADE为等边三角形,
∴∠DAF=60°,
∴∠ADF=30°.
∴AD∥BC,AD=BC,∠ADC=90°,
∵E为BC边中点,AO=DO,

∴AO=
| 1 |
| 2 |
| 1 |
| 2 |
∴AO=EC,AO∥EC,
∴四边形OAEC是平行四边形;
(2)如图1,连接OF,
∵四边形OAEC是平行四边形
∴AE∥OC,
∴∠DOC=∠OAF,
∠FOC=∠OFA,
∵OA=OF,
∴∠OAF=∠OFA,

∴∠DOC=∠FOC,
在△ODC与△OFC中,
|
∴△ODC≌△OFC(SAS),
∴∠OFC=∠ODC=90°,
∴OF⊥CF,
∴CF与 O相切;
(3)如图2,连接DE,
∵AD是直径,
∴∠AFD=90°,
∵点F为AE的中点,
∴DF为AE的垂直平分线,
∴DE=AD,
在△ABE与R△DCE中,
|
∴△ABE≌△DCE,
∴AE=DE,
∴AE=DE=AD,
∴三角形ADE为等边三角形,
∴∠DAF=60°,
∴∠ADF=30°.
看了 如图,四边形ABCD为矩形,...的网友还看了以下:
模数3齿数28齿宽30的容许力矩25.45N*M现在厚度加厚到60可以承载多大的力矩我查了米思米的 2020-04-06 …
我想问的是为什么不选右上(这道题的答案是左下)“标准对数视力表”对我们来说并不陌生,如图是视力表的 2020-04-26 …
具有过盈的配合称为( ),被常用于精确的定位配合中,或传递和承受大的扭矩和动载荷的部位.A.间隙配 2020-05-31 …
离合器后备系数大可以( )A.传递大的扭矩B.防止传动系过载C.使离合器操纵变轻 2020-05-31 …
大家看看我这个矩阵的证明哪里有问题已知A,B为n阶方阵,且B=B^2,A=B+E,证明A可逆,并求 2020-06-09 …
从0到无穷大的e(-x^2)怎么求和? 2020-06-14 …
矩阵平方差设方阵A满足A²-A-2E=O,求A的逆矩阵.答案是1/2(A-E).为啥不是1/2E, 2020-07-18 …
(2011•六盘水)“标准对数视力表”对我们来说并不陌生,如图是视力表的一部分,其中最上面较大的“ 2020-08-01 …
旋转圆盘的力矩计算公式?电机同心带动0.5公斤、直径60毫米的匀介质以3000rpm的速度转动,需 2020-08-02 …
“标准对数视力表”对我们来说并不陌生,如图是视力表的一部分,其中最上面较大的“E”与下面四个较小“E 2020-12-01 …