早教吧作业答案频道 -->数学-->
已知△ABC中,∠ACB=90°,∠A=60°,AC=6,点D为AC边上的一个动点,DE⊥AB,垂足为点E.(1)如图1,当BD恰好平分∠ABC时,求AD的长;(2)如图2,若点F为BD的中点,联结EF,EC,FC,判断△EFC的
题目详情
已知△ABC中,∠ACB=90°,∠A=60°,AC=6,点D为AC边上的一个动点,DE⊥AB,垂足为点E.
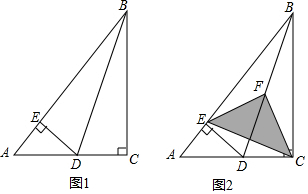
(1)如图1,当BD恰好平分∠ABC时,求AD的长;
(2)如图2,若点F为BD的中点,联结EF,EC,FC,判断△EFC的形状并加以证明;
(3)当△EFC的面积取得最小值时,求AD的长.

(1)如图1,当BD恰好平分∠ABC时,求AD的长;
(2)如图2,若点F为BD的中点,联结EF,EC,FC,判断△EFC的形状并加以证明;
(3)当△EFC的面积取得最小值时,求AD的长.
▼优质解答
答案和解析
 (1)如图1,当BD平分∠ABC时,
(1)如图1,当BD平分∠ABC时,
∵∠ACB=90°,DE⊥AB,
∴DC=DE,
设AD=x,则CD=ED=6-x,
∵∠A=60°,
∴∠ADE=30°,
∴AE=
AD=
x,
在Rt△ADE中,由勾股定理可得(
x)2+(6-x)2=x2,
解得x1=24-12
,x2=24+12
(舍去)
∴AD的长为24-12
;
(2)如图2,∵点F是BD的中点,∠DEB=∠DCB=90°,
∴EF=
BD=CF=BF,
∴∠EBF=∠BEF,∠FBC=∠FCB,
∴∠EFC=∠EFD+∠CFD=2∠EBF+2∠CBF=2∠ABC=60°,
∴△EFC是等边三角形;
(3)∵点D是线段AC上的动点,AC⊥BC,
∴根据垂线段最短,可得
当点D与点C重合时,BD最短,
此时CF也最短,即等边三角形EFC的面积最小,
此时,AD=AC=6.
 (1)如图1,当BD平分∠ABC时,
(1)如图1,当BD平分∠ABC时,∵∠ACB=90°,DE⊥AB,
∴DC=DE,
设AD=x,则CD=ED=6-x,
∵∠A=60°,
∴∠ADE=30°,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ADE中,由勾股定理可得(
| 1 |
| 2 |
解得x1=24-12
| 3 |
| 3 |
∴AD的长为24-12
| 3 |
(2)如图2,∵点F是BD的中点,∠DEB=∠DCB=90°,
∴EF=
| 1 |
| 2 |
∴∠EBF=∠BEF,∠FBC=∠FCB,
∴∠EFC=∠EFD+∠CFD=2∠EBF+2∠CBF=2∠ABC=60°,
∴△EFC是等边三角形;
(3)∵点D是线段AC上的动点,AC⊥BC,
∴根据垂线段最短,可得
当点D与点C重合时,BD最短,
此时CF也最短,即等边三角形EFC的面积最小,
此时,AD=AC=6.
看了 已知△ABC中,∠ACB=9...的网友还看了以下:
在人身意外伤害保险实务中,保险人区分和把握不可保意外伤害的要点是( )A.如果承保,将直接 2020-05-21 …
在人身意外伤害保险实务中,保险人区分和把握不可保意外伤害的要点是( ) A.如果承保, 2020-05-21 …
在人身意外伤害保险实务中,保险认区分和把握不可保意外伤害的要点是( )A.如果承保,是否将直接影 2020-05-22 …
如图已知A,B两点是反比例函数Y=X分之2的图像上任意两点,过A,B两点分别别做Y轴的如图,已知A 2020-06-14 …
如图,A、B两点在数轴上,这两点在数轴对应的数分别为-12、16.如图,A、B两点在数轴上,如图, 2020-07-21 …
如图所示的四种电场中,分别标记有a,b两点,其中a,b两点电场强度大小相等、方向相反的是()A.如 2020-07-21 …
如图,有一个圆柱图,B点在A点的下方,现将一根红线从A点沿圆柱体外侧缠绕到B点,圆柱(要写过程)如 2020-07-31 …
对四组不同数据进行统计,分别获得以下散点图,如果对它们的相关系数进行比较,下列结论中正确的是()A 2020-08-02 …
如图已知函数y=-1/2x+b的图像与x轴y轴分别交于点A、B与函数y=x的图像交于点M点M的如图已 2020-12-12 …
如图所示是皮带传动装置示意图,A为主动轮,B为从动轮.关于A轮边缘上P点、B轮边缘上如图4是一主动轮 2020-12-12 …