早教吧作业答案频道 -->数学-->
如图,已知四边形ABCD是矩形,cot∠ADB=34,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.(1)求线段BD的长;(2)设BE=x,△DEF的面积为y,求y关于x的函数关系式,并写出函数定义域;
题目详情
如图,已知四边形ABCD是矩形,cot∠ADB=
,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
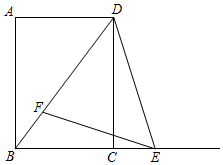
(1)求线段BD的长;
(2)设BE=x,△DEF的面积为y,求y关于x的函数关系式,并写出函数定义域;
(3)当△DEF为等腰三角形时,求线段BE的长.
| 3 |
| 4 |

(1)求线段BD的长;
(2)设BE=x,△DEF的面积为y,求y关于x的函数关系式,并写出函数定义域;
(3)当△DEF为等腰三角形时,求线段BE的长.
▼优质解答
答案和解析
(1)∵四边形ABCD是矩形,
∴∠A=90°,
在Rt△BAD中,cot∠ADB=
=
,AB=16,
∴AD=12∴BD=
=20;
(2)∵AD∥BC,
∴∠ADB=∠DBC,
∵∠DEF=∠ADB,
∴∠DEF=∠DBC,
∵∠EDF=∠BDE,
∴△EDF∽△BDE,
∴
=(
)2,
∵BC=AD=12,BE=x,
∴CE=|x-12|,
∵CD=AB=16
∴在Rt△CDE中,DE=
=
,
∵S△BDE=
×BE×CD=
•x•16=8x,
∴
=(
)2,
∴y=
,定义域为0<x≤24
(3)∵△EDF∽△BDE,
∴当△DEF是等腰三角形时,△BDE也是等腰三角形,
①当BE=BD时
∵BD=20,∴BE=20
②当DE=DB时,
∵DC⊥BE,∴BC=CE=12,
∴BE=24;
③当EB=ED时,
作EH⊥BD于H,则BH=
BD=10,cos∠HBE=cos∠ADB,
即
=
∴
=
,
解得:BE=
;
综上所述,当△DEF时等腰三角形时,线段BE的长为20或24或
.
∴∠A=90°,
在Rt△BAD中,cot∠ADB=
| AD |
| AB |
| 3 |
| 4 |
∴AD=12∴BD=
| AD2+AB2 |
(2)∵AD∥BC,
∴∠ADB=∠DBC,
∵∠DEF=∠ADB,
∴∠DEF=∠DBC,
∵∠EDF=∠BDE,
∴△EDF∽△BDE,
∴
| S△DEF |
| S△BDE |
| DE |
| BD |
∵BC=AD=12,BE=x,
∴CE=|x-12|,
∵CD=AB=16
∴在Rt△CDE中,DE=
| 162+(x-12)2 |
| x2-24x+400 |
∵S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| y |
| 8x |
| ||
| 20 |
∴y=
| x3-24x2+400x |
| 50 |
(3)∵△EDF∽△BDE,
∴当△DEF是等腰三角形时,△BDE也是等腰三角形,
①当BE=BD时
∵BD=20,∴BE=20
②当DE=DB时,
∵DC⊥BE,∴BC=CE=12,
∴BE=24;
③当EB=ED时,
作EH⊥BD于H,则BH=
| 1 |
| 2 |
即
| AD |
| BD |
| BH |
| BE |
∴
| 12 |
| 20 |
| 10 |
| BE |
解得:BE=
| 50 |
| 3 |
综上所述,当△DEF时等腰三角形时,线段BE的长为20或24或
| 50 |
| 3 |
看了 如图,已知四边形ABCD是矩...的网友还看了以下:
八年级矩形几何矩形ABCD的长为5,宽为3,点E,F将AC三等分矩形ABCD的长为5,宽为3,点E, 2020-03-30 …
在平行四边形ABCD中,点E,F分别是线段AD,BC上的两动点,点E从点A向D运动在平行四边形AB 2020-05-13 …
已知,如图,在正方形ABCD中,点E,F分别在AB上和AD的延长线上,且BE=DF,连接EF,G为 2020-05-15 …
如图,将变长为4cm的正方形纸片ABCD沿EF折叠(点E,F分别在边AB,CD上),使点B(字数限 2020-05-15 …
已知抛物线Y=aX2+bx+c经过点A(0,3)B(1,0) C(5,0)三点 1.求抛物线解析式 2020-05-15 …
△ABC是边长为4的等边三角形,以BC为底边做一个顶角为120°的等腰三角形△DBE,以D为顶点作 2020-05-17 …
已知点E,F为长方形ABCD的边上的点,且E(1,0),F(4,3),有知长方形的长为6,宽为4, 2020-05-17 …
如图长方形纸片ABCD,点E,F如图,长方形纸片ABCD,点E,F分别在AB,CD上,连接EF.将 2020-07-21 …
如何求证C,D,E,F四点共圆.以知:圆1与圆2相交与点A,B,点P在BA的延长线上,割线PCD交 2020-07-31 …
矩形ABCD中,AB=4,AD=3,P,Q是对角线BD上不重合的两点,点P关于直线AD,AB的对称点 2020-12-25 …