如图，在菱形ABCD中，过点B作BE⊥AD，BF⊥CD，垂足分别为点E，F，延长BD至G，使得DG=BD，连结EG，FG，若AE=DE，则EGAB=．

Question

如图，在菱形ABCD中，过点B作BE⊥AD，BF⊥CD，垂足分别为点E，F，延长BD至G，使得DG=BD，连结EG，FG，若AE=DE，则 (EG)/(AB)=___．

Answer 1

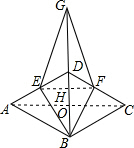如图，连接AC、EF，
在菱形ABCD中，AC⊥BD，
∵BE⊥AD，AE=DE，
∴AB=BD，
又∵菱形的边AB=AD，
∴△ABD是等边三角形，
∴∠ADB=60°，
设EF与BD相交于点H，AB=4x，
∵AE=DE，
∴由菱形的对称性，CF=DF，
∴EF是△ACD的中位线，
∴DH=(1)/(2)DO=(1)/(4)BD=x，
在Rt△EDH中，EH=√(3)DH=√(3)x，
∵DG=BD，
∴GH=BD+DH=4x+x=5x，
在Rt△EGH中，由勾股定理得，EG=√(EH2+GH2)=√((√(3)x)2+(5x)2)=2√(7)x，
所以，(EG)/(AB)=(2√(7)x)/(4x)=(√(7))/(2)．
故答案为：(√(7))/(2)．