如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FE=FE；②AH=2CD；③BC•AD=2AE2；④∠DFE=2∠DAC；⑤若连接CH，则CH∥EF，其中正确的

Question

如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FE=FE；②AH=2CD；③BC•AD=

√(2)AE²；④∠DFE=2∠DAC；⑤若连接CH，则CH∥EF，其中正确的个数为（　　）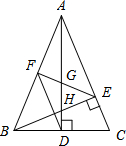

A. 2个

B. 3个

C. 4个

D. 5个

Answer 1

∵在△ABC中，AD和BE是高，
∴∠ADB=∠AEB=∠CEB=90°，
∵点F是AB的中点，
∴FD=(1)/(2)AB，
∵∠ABE=45°，
∴△ABE是等腰直角三角形，
∴AE=BE，
∵点F是AB的中点，
∴FE=(1)/(2)AB，
∴FD=FE，①正确；

∵∠CBE=∠BAD，∠CBE+∠C=90°，∠BAD+∠ABC=90°，
∴∠ABC=∠C，
∴AB=AC，
∵AD⊥BC，
∴BC=2CD，∠BAD=∠CAD=∠CBE，
在△AEH和△BEC中，

∠AEH=∠CEB

AE=BE

∠EAH=∠CBE

，
∴△AEH≌△BEC（ASA），
∴AH=BC=2CD，故②正确；

∵∠BAD=∠CBE，∠ADB=∠CEB，
∴△ABD～△BCE，
∴(BC)/(AB)=(BE)/(AD)，即BC•AD=AB•BE，
∵√(2)AE²=AB•AE=AB•BE，BC•AD=AC•BE=AB•BE，
∴BC•AD=√(2)AE²，故③正确；

∵△ABE是等腰直角三角形，
∴∠BAE=45°，
又∵AB=AC，AD⊥BC，
∴AD平分∠BAC，
∴∠BAD=∠CAD=22.5°，
∵AF=DF，
∴∠FAD=∠FDA=22.5°，
∴∠BFD=45°，
∴∠DFE=90°-45°=45°，
∴∠DFE=2∠DAC，故④正确；

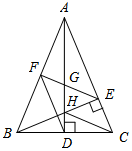
∵AB=AC，∠BAH=∠CAH，AH=AH，
∴△ABH≌△ACH，
∴∠ACH=∠ABH=45°，
又∵Rt△AEF中，∠AEF=45°，
∴CH∥EF，故⑤正确．
故选：D．