早教吧作业答案频道 -->数学-->
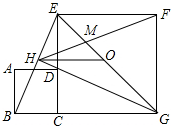
如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE;②BG=EG;③△MFG为等腰三角形;④DE:AB
题目详情
如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:
①GH⊥BE;②BG=EG;③△MFG为等腰三角形;④DE:AB=1+
,
其中正确结论的序号为___.
①GH⊥BE;②BG=EG;③△MFG为等腰三角形;④DE:AB=1+
| | 2 |
其中正确结论的序号为___.

▼优质解答
答案和解析
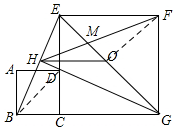 ∵正方形ABCD的边CD在正方形ECGF的边CE上,
∵正方形ABCD的边CD在正方形ECGF的边CE上,
∴∠BCE=∠DCG=90°,BC=DC,EC=GC,
∴△BCE≌△DCG(SAS),
∴∠CGD=∠CEB,
又∵∠CDG=∠HDE,
∴∠EHD=∠GCD=90°,
∴GH⊥BE,故①正确;
∵∠EGC的平分线GH过点D,
∴∠BGH=∠EGH,
∵GH⊥BE,
∴∠BHG=∠EHG=90°,
∴△BGH≌△EGH(ASA),
∴BG=EG,故②正确;
∵BG=EG,GH⊥BE,
∴H为BE的中点,
又∵O是EG的中点,
∴HO是△BEG的中位线,
∴HO=
BG,HO∥BG,
∴∠MOH=∠EGC=45°,
如图,连接FO,
∵O是EG的中点,
∴等腰Rt△EFG中,OF=
EG,∠OFG=45°,
∴OH=OF,
∴∠OHF=∠OFH,
∴∠MHO+∠HOM=∠OFH+∠OFG,即∠FMG=∠MFG,
∴FG=MG,即△MFG是等腰三角形,故③正确;
如图,连接BD,
∵HG垂直平分BE,
∴DE=DB,
∵Rt△ABD中,DB:AB=
:1,
∴DE:AB=
:1,故④错误;
故答案为:①②③
 ∵正方形ABCD的边CD在正方形ECGF的边CE上,
∵正方形ABCD的边CD在正方形ECGF的边CE上,∴∠BCE=∠DCG=90°,BC=DC,EC=GC,
∴△BCE≌△DCG(SAS),
∴∠CGD=∠CEB,
又∵∠CDG=∠HDE,
∴∠EHD=∠GCD=90°,
∴GH⊥BE,故①正确;
∵∠EGC的平分线GH过点D,
∴∠BGH=∠EGH,
∵GH⊥BE,
∴∠BHG=∠EHG=90°,
∴△BGH≌△EGH(ASA),
∴BG=EG,故②正确;
∵BG=EG,GH⊥BE,
∴H为BE的中点,
又∵O是EG的中点,
∴HO是△BEG的中位线,
∴HO=
| 1 |
| 2 |
∴∠MOH=∠EGC=45°,
如图,连接FO,
∵O是EG的中点,
∴等腰Rt△EFG中,OF=
| 1 |
| 2 |
∴OH=OF,
∴∠OHF=∠OFH,
∴∠MHO+∠HOM=∠OFH+∠OFG,即∠FMG=∠MFG,
∴FG=MG,即△MFG是等腰三角形,故③正确;
如图,连接BD,
∵HG垂直平分BE,
∴DE=DB,
∵Rt△ABD中,DB:AB=
| 2 |
∴DE:AB=
| 2 |
故答案为:①②③
看了 如图,正方形ABCD的边CD...的网友还看了以下:
海浪的传播速度跟海水的深度有关,其关系式为v=gh,式中h为海水的深度,g为重力加速度.现有剖面如 2020-05-16 …
高中曲线方程的一道题..设动点P在直线X=1上,O为原点.以OP为直角边,O为直角顶点做等腰RT三 2020-05-23 …
一个长方形有几组互相平行的边?o迈伽,快回答! 2020-06-03 …
海浪的传播速度跟海水的深度有关,其关系式为v=gh,式中h为海水的深度,g为重力加速度.现有剖面如 2020-06-05 …
1.已知:在正方形ABCD中,点E,F,G,H分别在AB,BC,CD和DA上,且EG⊥FH,求证: 2020-06-05 …
(2003•三明)已知:如图,边长为2的正五边形ABCDE内接于⊙O,AB、DC的延长线交于点F, 2020-08-03 …
(2007•南平)如图,在路边O处安装路灯,路面宽ED为16米,灯柱OB与路边的距离OE为2米,且灯 2020-11-12 …
(2007•南平)如图,在路边O处安装路灯,路面宽ED为16米,灯柱OB与路边的距离OE为2米,且灯 2020-11-12 …
如图,在路边O处安装路灯,路面宽ED为16米,灯柱OB与路边的距离OE为2米,且灯柱OB与灯杆AB成 2020-12-21 …
如图(1),(2),牧童在点A处放牛,其家住在点B处,点A、B到河岸CD的距离分别为AC和BD.(1 2020-12-30 …