早教吧作业答案频道 -->数学-->
直线y=-x+2与X轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB.(1)求AC的解析式;(2)若在OA的延长线上取一点P,作PQ⊥BP,交直线AC于Q,试探究BP与PQ的数最关系;并证明你的结论;(3)
题目详情
直线y=-x+2与X轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB.
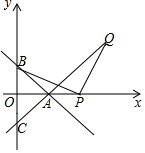
(1)求AC的解析式;
(2)若在OA的延长线上取一点P,作PQ⊥BP,交直线AC于Q,试探究BP与PQ的数最关系;并证明你的结论;
(3)在(2)的前提下,作PM⊥QC于M,求证:
的值是定值,并求出这一定值.

(1)求AC的解析式;
(2)若在OA的延长线上取一点P,作PQ⊥BP,交直线AC于Q,试探究BP与PQ的数最关系;并证明你的结论;
(3)在(2)的前提下,作PM⊥QC于M,求证:
| MQ-AC |
| PM |
▼优质解答
答案和解析
(1)在y=-x+2中,令y=0可求得x=2,令x=0可求得y=2,
∴A(2,0),B(0,2),
∵OC=OB,
∴点C坐标(0,-2),
设直线AC的解析式为y=kx+b,
把B、C两点坐标代入可得
,解得
,
∴直线AC的解析式为y=x-2;
(2)如图1中,结论:PB=PQ.
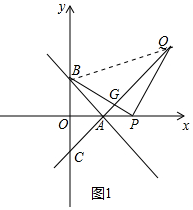
证明如下
:连接BQ,AQ与PB交于点G.
∵OA=OB=OC,
∴∠OAB=∠OBA=∠OAC=∠OCA=45°,
∴∠CAB=∠BAQ=90°,
∵PB⊥PQ,
∴∠BAG=∠QPG=90°,
∵∠AGB=∠PGQ,
∴△ABG∽△PQG,
∴
=
,
∴
=
,
∵∠BGQ=∠AGP,
∴△BGQ∽△AGP,
∴∠QBG=∠GAP,
∵∠OAC=∠PAG=45°,
∴∠PBQ=∠PAG=45°,
∵∠BPQ=90°,
∴∠PBQ=∠PQB=45°,
∴PB=PQ;
(3)证明:
如图2,作PG⊥PA交PA的延长线于G.
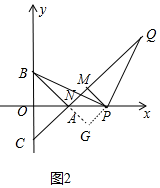
由(2)可知,∠PAM=∠PAG=45°,
∵PM⊥AQ,PG⊥AG,
∴PM=PG,
∵∠G=∠GAM=∠PMA=90°,
∴四边形AMPG是矩形,
∵PM=PG,
∴四边形AMPG是正方形,
∴AG=PM,
在△PMQ和△PGB中,
,
∴△PMQ≌△PGB(AAS),
∴MQ=BG,
∵AB=AC,
∴
=
=
=1.
(1)在y=-x+2中,令y=0可求得x=2,令x=0可求得y=2,
∴A(2,0),B(0,2),
∵OC=OB,
∴点C坐标(0,-2),
设直线AC的解析式为y=kx+b,
把B、C两点坐标代入可得
|
|
∴直线AC的解析式为y=x-2;
(2)如图1中,结论:PB=PQ.

证明如下
:连接BQ,AQ与PB交于点G.
∵OA=OB=OC,
∴∠OAB=∠OBA=∠OAC=∠OCA=45°,
∴∠CAB=∠BAQ=90°,
∵PB⊥PQ,
∴∠BAG=∠QPG=90°,
∵∠AGB=∠PGQ,
∴△ABG∽△PQG,
∴
| BG |
| GQ |
| AG |
| PG |
∴
| BG |
| AG |
| GQ |
| PG |
∵∠BGQ=∠AGP,
∴△BGQ∽△AGP,
∴∠QBG=∠GAP,
∵∠OAC=∠PAG=45°,
∴∠PBQ=∠PAG=45°,
∵∠BPQ=90°,
∴∠PBQ=∠PQB=45°,
∴PB=PQ;
(3)证明:
如图2,作PG⊥PA交PA的延长线于G.

由(2)可知,∠PAM=∠PAG=45°,
∵PM⊥AQ,PG⊥AG,
∴PM=PG,
∵∠G=∠GAM=∠PMA=90°,
∴四边形AMPG是矩形,
∵PM=PG,
∴四边形AMPG是正方形,
∴AG=PM,
在△PMQ和△PGB中,
|
∴△PMQ≌△PGB(AAS),
∴MQ=BG,
∵AB=AC,
∴
| MQ-AC |
| PM |
| BG-AB |
| PM |
| AG |
| PM |
看了 直线y=-x+2与X轴、y轴...的网友还看了以下:
已知点p的坐标是(a-2,2a+1),若点p在x轴上,则a等于多少?若点p在y轴上,则a等于多少? 2020-04-06 …
很简单但是我想不通玻璃管内活塞P下方封闭着空气,P上有细线系住,线上端悬于O点,P的上方有高h的水 2020-05-17 …
如图,点A是双曲线y=8x(x>0)上的一点,P为x轴正半轴上的一点,且点P的坐标为(4,0),将 2020-05-21 …
急救!已知三角形ABC,AB=AC,P为BC上一点,试猜想点P到两腰距离之和等于什么?并加以证明, 2020-06-06 …
已知等边三角形ABC内接于⊙O,P为⊙O上异于A、B、C的动点.当点P为弦BC所对的劣弧上一点时( 2020-06-23 …
某校课外小组在离湖面7米高的观测点A处,看湖面上空一热气球P的仰角为37度,看P在湖中倒影P'的府 2020-06-30 …
一弹簧秤的称盘质量M1=1.5Kg,盘内放一物体P,P的质量M2=10.5Kg.弹簧质量不计.其劲 2020-06-30 …
如图所示,物体P静止于固定的斜面上,P的上表面水平.现把物体Q轻轻地叠放在P上,则()A.P向下滑 2020-07-07 …
(2013•广东)如图,物体P静止于固定的斜面上,P的上表面水平.现把物体Q轻轻地叠放在P上,则( 2020-07-07 …
直线MN上有P'、O、P、Q四点,质点A、B在某时刻分别位于P点和Q点,并具有相同的速直线MN上有 2020-07-09 …