早教吧作业答案频道 -->数学-->
如图,在△ABC中,点E在AC上,∠AEB=∠ABC.(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线
题目详情
如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?
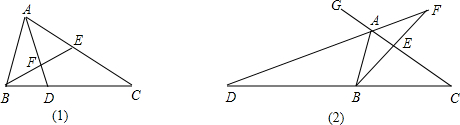
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?

▼优质解答
答案和解析
(1)∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC;
(2)探究(1)中结论仍成立;
理由:∵AD平分∠BAG,
∴∠BAD=∠GAD,
∵∠FAE=∠GAD,
∴∠FAE=∠BAD,
∵∠EFD=∠AEB-∠FAE,∠ADC=∠ABC-∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC.
∴∠BAD=∠DAC,
∵∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC;
(2)探究(1)中结论仍成立;
理由:∵AD平分∠BAG,
∴∠BAD=∠GAD,
∵∠FAE=∠GAD,
∴∠FAE=∠BAD,
∵∠EFD=∠AEB-∠FAE,∠ADC=∠ABC-∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC.
看了 如图,在△ABC中,点E在A...的网友还看了以下:
设A为三阶实对称矩阵,且A2+2A=0,R(A)=2.(1)求A的全部特征值;(2)证明:当k>2 2020-04-13 …
对于有理数a、b,定义运算:“⊗”,a⊗b=ab-a-b-2.(1)计算:(-2)⊗3的值;(2) 2020-06-06 …
设A为三阶实对称矩阵,且满足A2+2A=0,已知A的秩r(A)=2.(1)求A的全部特征值;(2) 2020-06-18 …
已知函数f(x)=|x+a|+|x-2|.(1)当a=1时,求不等式f(x)≥5的解集;(2)若f 2020-07-29 …
如图①,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A′的位置.通过计算我们知道:2∠ 2020-07-31 …
(1)已知两个连续奇数的平方差为2000,则这两个连续奇数可以是.(2)已知(2000-a)(19 2020-08-03 …
说出下面不等式的变形是根据不等式的哪一个基本性质.(1)如果3a<6,那么a<2.(2)如果a-3 2020-08-03 …
下列给出的输入语句、输出语句和赋值语句正确的个数是()个(1)输入语句INPUTa;b;c(2)输出 2020-12-31 …
下列给出的输入语句、输出语句和赋值语句正确的个数是()个(1)输入语句INPUTa;b;c(2)输出 2020-12-31 …
对于有理数a、b,定义运算:“⊕”,a⊕b=a×b-a-b-2.(1)计算:(-2)⊕3的值;(2) 2021-01-20 …