早教吧作业答案频道 -->数学-->
请你参与下面探究过程,完成所提出的问题.(1)探究1:如图1,P是△ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70°,则∠BPC=度;(2)探究2:如图2,P是△ABC的外角∠DBC与外角
题目详情
请你参与下面探究过程,完成所提出的问题.
(1)探究1:如图1,P是△ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70°,则∠BPC=___度;
(2)探究2:如图2,P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系?并说明理由.
(3)拓展:如图3,P是四边形ABCD的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D=α.
①直接写出∠BPC与α的数量关系;
②根据α的值的情况,判断△BPC的形状(按角分类).
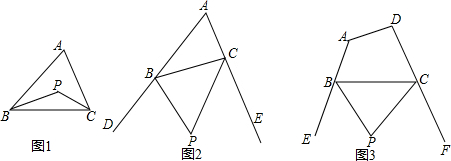
(1)探究1:如图1,P是△ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70°,则∠BPC=___度;
(2)探究2:如图2,P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系?并说明理由.
(3)拓展:如图3,P是四边形ABCD的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D=α.
①直接写出∠BPC与α的数量关系;
②根据α的值的情况,判断△BPC的形状(按角分类).

▼优质解答
答案和解析
(1)∵∠A=70°,
∴∠ABC+∠ACB=110°,
∵BP、CP是角平分线,
∴∠ABC=2∠PBC,∠ACB=2∠BCP,
∴∠PBC+∠BCP=55°,
∵∠PBC+∠BCP+∠BPC=180°,
∴∠BPC=125°,
故答案为:125;
(2)∵BP,CP分别是外角∠DBC,∠ECB的平分线,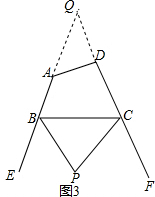
∴∠PBC+∠PCB=
(∠DBC+∠ECB)=
(180°-∠A),
在△PBC中,∠P=180°-
(180°-∠A)=90°-
∠A.
(3)如图3,
①延长BA、CD于Q,
则∠P=90°-
∠Q,
∴∠Q=180°-2∠P,
∴∠BAD+∠CDA
=180°+∠Q
=180°+180°-2∠P
=360°-2∠P,
∴∠P=180°-
α;
②当0<α<180时,△BPC是钝角三角形,
当α=180时,△BPC是直角三角形,
当α>180时,△BPC是鋭角三角形.
∴∠ABC+∠ACB=110°,
∵BP、CP是角平分线,
∴∠ABC=2∠PBC,∠ACB=2∠BCP,
∴∠PBC+∠BCP=55°,
∵∠PBC+∠BCP+∠BPC=180°,
∴∠BPC=125°,
故答案为:125;
(2)∵BP,CP分别是外角∠DBC,∠ECB的平分线,

∴∠PBC+∠PCB=
| 1 |
| 2 |
| 1 |
| 2 |
在△PBC中,∠P=180°-
| 1 |
| 2 |
| 1 |
| 2 |
(3)如图3,
①延长BA、CD于Q,
则∠P=90°-
| 1 |
| 2 |
∴∠Q=180°-2∠P,
∴∠BAD+∠CDA
=180°+∠Q
=180°+180°-2∠P
=360°-2∠P,
∴∠P=180°-
| 1 |
| 2 |
②当0<α<180时,△BPC是钝角三角形,
当α=180时,△BPC是直角三角形,
当α>180时,△BPC是鋭角三角形.
看了 请你参与下面探究过程,完成所...的网友还看了以下:
1、下列选项正确的是()A、x=3是不等式2x>1的解B、x=3是不等式2x>1的唯一解C、X=3不 2020-03-31 …
五题数学题,解题过程要完整,都是完全平方式和平方差,有的是直接计算哦!1.(a+5b)(a-4b) 2020-04-27 …
1.什么叫从集合a到集合b的函数?2.判断下列是不是从集合a到集合b的函数题1--a={1/2,1 2020-05-13 …
一,已知A={x|x=k/4+1/2,k∈Z} B={x|x=k/8+1/4,k∈Z}那么集合A与 2020-05-16 …
发生赤潮的海水颜色与( )的种类和数量无关第十一届环保知识竞赛的题B海洋鱼类 C海洋植物 2020-05-16 …
下图1中,ab表示一个细胞周期,cd表示另一个细胞周期.图2中,按箭头方向,表示细胞周期.从图中所 2020-05-17 …
特性音程及解决方面的题.B和声大调的特性音程及解决.还有降E,F,E,降A的特性音程,谁知道啊,帮 2020-05-17 …
给出三个命题:1.点P(B,A)在抛物线Y=X^2+1上;2.点A(1,3)能在抛物线Y=AX^2 2020-05-17 …
第一题:设A=(0,1],B=[-1,0],求A∩B第二题:设A={1,2,3,4,5,6,7,8 2020-05-22 …
基本不等式解题时,除了求最值,什么时候要求左右一方为定值求最值问题,一定要求左右一方为定值,但看如 2020-05-23 …