早教吧作业答案频道 -->数学-->
如图1所示,在边长为1的正方形ABCD中,P是BC边上一动点,AP的延长线与∠ABC的外角平分线交于E,∠EAF=45°,且AF交∠ADC的外角平分线交于F,把△ADF绕A旋转至△ABQ.(Ⅰ)如图1所示,当BE=DF时
题目详情
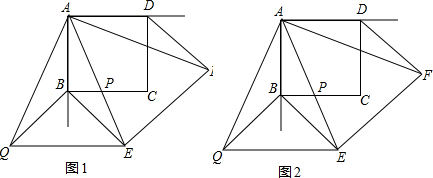
如图1所示,在边长为1的正方形ABCD中,P是BC边上一动点,AP的延长线与∠ABC的外角平分线交于E,∠EAF=45°,且AF交∠ADC的外角平分线交于F,把△ADF绕A旋转至△ABQ.
(Ⅰ)如图1所示,当BE=DF时,求BQ的长;
(Ⅱ)如图2所示.
(1)请探究线段BE,DF,EF之间的数量关系,并证明.
(2)当点P在BC边上运动时,记BP=x(0<x<1),S△BEQ=y,探究y是否随着x的变化而变化,若不变化,求出y的值,若变化,求出y与x的函数关系式.
(Ⅰ)如图1所示,当BE=DF时,求BQ的长;
(Ⅱ)如图2所示.
(1)请探究线段BE,DF,EF之间的数量关系,并证明.
(2)当点P在BC边上运动时,记BP=x(0<x<1),S△BEQ=y,探究y是否随着x的变化而变化,若不变化,求出y的值,若变化,求出y与x的函数关系式.

▼优质解答
答案和解析
(Ⅰ)∵四边形ABCD是正方形,
∴AB=AD=1,∠ABC=∠ADC=∠BAD=90°.
∵BE、DF分别是正方形ABCD的外角平分线,
∴∠EBC=∠CDF=45°.
∴∠ABE=∠ADF=135°.
在△ABE和△ADF中,由于
,
∴△ADF≌△ABE.
∴∠BAE=∠DAF
∵∠EAF=45°,
∴∠DAF=
(90°-45°)=22.5°.
∵∠ADF=135°,
∴∠AFD=22.5°,
∴∠DAF=∠DFA,
∴AB=DF=1.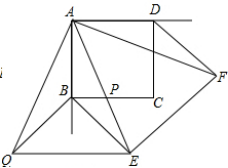
∵△ADF绕A旋转至△ABQ,
∴△ADF≌△ABQ,
∴BQ=DF=1.
(Ⅱ)(1)BE2+DF2=EF2.
证明:∵△ADF≌△ABQ,
∴BQ=DF,AQ=AF,∠QAB=∠DAF=22.5°,∠ADF=∠ABQ=135°,
又∵∠ABE=135°,
∴∠QBE=360°-∠ABQ-∠ABE=90°,
在RT△BQE中,BE2+BQ2=QE2.即BE2+DF2=QE2.
∵∠QAB=∠BAE=∠DAF=22.5°,
∴∠QAE=45°
∴∠QAE=∠EAF.
在△QAE和△FAE中,由于
,
∴△QAE≌△FAE,
∴QE=EF.
∴BE2+DF2=EF2.
(2)当点P在BC边上运动时,
∵∠ADF=∠ABE=135°,
∴∠BAE+∠BEA=45°,
又∵∠DAF+∠BAE=45°,
∴∠DAF=∠AEB.
∴△ABE∽△FDA.
由于△ADF≌△ABQ,
∴△ABE∽△QBA.
∴
=
即BQ×BE=1.
∵△BQE为直角三角形,
∴y=S△QBE=
×BQ×BE=
.
所以y不随x(0<x<1)的变化而变化,恒等于
.
∴AB=AD=1,∠ABC=∠ADC=∠BAD=90°.
∵BE、DF分别是正方形ABCD的外角平分线,
∴∠EBC=∠CDF=45°.
∴∠ABE=∠ADF=135°.
在△ABE和△ADF中,由于
|
∴△ADF≌△ABE.
∴∠BAE=∠DAF
∵∠EAF=45°,
∴∠DAF=
| 1 |
| 2 |
∵∠ADF=135°,
∴∠AFD=22.5°,
∴∠DAF=∠DFA,
∴AB=DF=1.

∵△ADF绕A旋转至△ABQ,
∴△ADF≌△ABQ,
∴BQ=DF=1.
(Ⅱ)(1)BE2+DF2=EF2.
证明:∵△ADF≌△ABQ,
∴BQ=DF,AQ=AF,∠QAB=∠DAF=22.5°,∠ADF=∠ABQ=135°,
又∵∠ABE=135°,
∴∠QBE=360°-∠ABQ-∠ABE=90°,
在RT△BQE中,BE2+BQ2=QE2.即BE2+DF2=QE2.
∵∠QAB=∠BAE=∠DAF=22.5°,
∴∠QAE=45°
∴∠QAE=∠EAF.

在△QAE和△FAE中,由于
|
∴△QAE≌△FAE,
∴QE=EF.
∴BE2+DF2=EF2.
(2)当点P在BC边上运动时,
∵∠ADF=∠ABE=135°,
∴∠BAE+∠BEA=45°,
又∵∠DAF+∠BAE=45°,
∴∠DAF=∠AEB.
∴△ABE∽△FDA.
由于△ADF≌△ABQ,

∴△ABE∽△QBA.
∴
| BQ |
| AB |
| AB |
| BE |
即BQ×BE=1.
∵△BQE为直角三角形,
∴y=S△QBE=
| 1 |
| 2 |
| 1 |
| 2 |
所以y不随x(0<x<1)的变化而变化,恒等于
| 1 |
| 2 |
看了 如图1所示,在边长为1的正方...的网友还看了以下:
在概率论中:P(A-B)的数学意义是什么?看到有人这样解释:当B属于A时,P(A-B)=P(A)- 2020-05-16 …
(2008年)假定现值为P,等额年金为A,年利率为i,那么n年后的本利和F的计算公式为 ( )。A. 2020-05-19 …
已知命题p:1属于集合x2小于a,命题q:2属于x2小于a若p或q为真命题,求实数a的取值范围若p 2020-06-12 …
已知AB‖CD,直线EF分别交AB,CD于点E,F,角∠BEF的平行线宇∠DEF的平行线相较于点F 2020-06-24 …
关于齐次线性微分方程的通解设非齐次线性微分方程y'+P(x)y=Q(x)有两个不同的解a(x),b 2020-06-27 …
B属于A,C属于A,且P(A)=0.9,P(B非+C非)=0.8,那么P(A-BC)=zywzzy 2020-07-19 …
设lim(x趋于a)[f(x)-f(a)/(x-a)^2]=-1,则f(x)在x=a处取得极大值为 2020-07-20 …
a的负1次方为什么等于a的1次方分之一,这是公式吗?怎么推导?以及a的负p次方为什么等于a的p次方分 2021-01-13 …
某公司的年销售额为a元,成本为销售额的60%,税额和其他费用合计为销售额的P%.(1)用关于a、P的 2021-01-13 …
某公司的年销售额为a元,成本为销售额的60%,税额和其他费用合计为销售额的P%.(1)用关于a、P的 2021-01-13 …