早教吧作业答案频道 -->数学-->
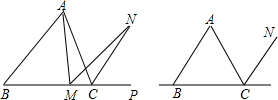
如图,在等边三角形ABC中,M是BC边(不含端点B,C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点,已知∠AMN=60°,(1)求证:AM=MN;(2)当M在直线BC上运动时,上述结论是否成
题目详情
如图,在等边三角形ABC中,M是BC边(不含端点B,C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点,已知∠AMN=60°,
(1)求证:AM=MN;
(2)当M在直线BC上运动时,上述结论是否成立?若成立,请画图证明.
(1)求证:AM=MN;
(2)当M在直线BC上运动时,上述结论是否成立?若成立,请画图证明.

▼优质解答
答案和解析
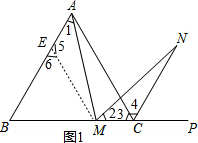 (1)证明:如图1,在AB上截取EA=MC,连接EM,得△AEM,
(1)证明:如图1,在AB上截取EA=MC,连接EM,得△AEM,
∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB-∠B,∠AMN=∠B=60°,
∴∠1=∠2.
又∵CN平分∠ACP,∠4=
∠ACP=60°,
∴∠MCN=∠3+∠4=120°…①
又∵BA=BC,EA=MC,
∴BA-EA=BC-MC,即BE=BM,
∴△BEM为等边三角形,
∴∠6=60°,
∴∠5=180°-∠6=120°,
∴由①②得∠MCN=∠5.
在△AEM和△MCN中,
,
∴△AEM≌△MCN (ASA),
∴AM=NM;
(2) AM=NM仍然成立,理由如下:
如图2,连接AN,CN,
∵△ABC是等边三角形,
∴∠ACB=∠BAC=60°,AB=AC.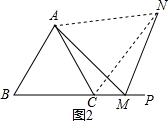
∵CN为等边△ABC的外角∠ACP的平分线,
∴∠ACN=∠NCP=
∠ACP=60°,
∴∠AMN=∠ACN=60°,
∴A、C、M、N四点共圆,
∴∠NAM=∠NCM=∠BAC=60°,
∴∠BAC+∠CAM=∠NAM+∠CAM,即∠BAM=∠CAN,
∵AB=AC,∠ABM=∠ACN=60°,
在△ABM与△ACN中,
,
∴△ABM≌△ACN,
∴AN=AM,
∵∠AMN=60°,
∴△AMN是等边三角形,
∴AM=NM.
 (1)证明:如图1,在AB上截取EA=MC,连接EM,得△AEM,
(1)证明:如图1,在AB上截取EA=MC,连接EM,得△AEM,∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB-∠B,∠AMN=∠B=60°,
∴∠1=∠2.
又∵CN平分∠ACP,∠4=
| 1 |
| 2 |
∴∠MCN=∠3+∠4=120°…①
又∵BA=BC,EA=MC,
∴BA-EA=BC-MC,即BE=BM,
∴△BEM为等边三角形,
∴∠6=60°,
∴∠5=180°-∠6=120°,
∴由①②得∠MCN=∠5.
在△AEM和△MCN中,
|
∴△AEM≌△MCN (ASA),
∴AM=NM;
(2) AM=NM仍然成立,理由如下:
如图2,连接AN,CN,
∵△ABC是等边三角形,
∴∠ACB=∠BAC=60°,AB=AC.

∵CN为等边△ABC的外角∠ACP的平分线,
∴∠ACN=∠NCP=
| 1 |
| 2 |
∴∠AMN=∠ACN=60°,
∴A、C、M、N四点共圆,
∴∠NAM=∠NCM=∠BAC=60°,
∴∠BAC+∠CAM=∠NAM+∠CAM,即∠BAM=∠CAN,
∵AB=AC,∠ABM=∠ACN=60°,
在△ABM与△ACN中,
|
∴△ABM≌△ACN,
∴AN=AM,
∵∠AMN=60°,
∴△AMN是等边三角形,
∴AM=NM.
看了 如图,在等边三角形ABC中,...的网友还看了以下:
如图,已知A、B、C三点在一条直线上,分别以AB、BC为边在AC同侧作等边三角形ABD和等边三角形B 2020-03-31 …
设A,B,C表示三个随机事件,试以A,B,C的运算来表示以下事件:(1)A,B,C不全发生;(2) 2020-04-05 …
高二数学的空间向量问题~~~急!已知空间三个非零向量a,b,c不共面,向量AB=a+2b-c,向量 2020-05-13 …
a,b,c是三个不同的自然数,且a,b,c不为0,若A=a×b×c,那么,A至少有几个因数用五年级 2020-06-08 …
如果a乘3/4=b乘1/2=c乖2/5(a,b,c不等于0,)那么a,b,c三个的数是几?选择题如 2020-06-20 …
(数学题)设A,B,C为三个事件,用A,B,C表示下列事件:1)A,B,C中恰有一个发生2)A,B 2020-06-27 …
高一数学:已知集合A,B,C(不必相异)的并集A∪B∪C={1,2,3,4,5},且1∈A∪B已知 2020-07-20 …
有三种消化液,ABC,他们都不是唾液和肠液,A和C不能消化淀粉,A能促进B消化脂肪,而B和C能消化蛋 2020-11-04 …
小学六年级数学题已知ax6/5=9/10xb=13/13xc=1,并且a,b,c,不等于0,试把a, 2020-11-20 …
“三个数a、b、c不都为0”的否定为()A.c不都是为0B.c至多有一个为0C.c至少有一个为0D. 2020-12-14 …