早教吧作业答案频道 -->数学-->
在等边三角形ABC中,E为直线AB上一点,连接EC.ED与直线BC交于点D,ED=EC.(1)如图1,AB=1,点E是AB的中点,求BD的长;(2)点E是AB边上任意一点(不与AB边的中点和端点重合),依题意,将
题目详情
在等边三角形ABC中,E为直线AB上一点,连接EC.ED与直线BC交于点D,ED=EC.
(1)如图1,AB=1,点E是AB的中点,求BD的长;
(2)点E是AB边上任意一点(不与AB边的中点和端点重合),依题意,将图2补全,判断AE与BD间的数量关系并证明;
(3)点E不在线段AB上,请在图3中画出符合条件的一个图形.
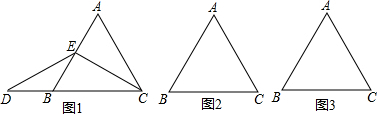
(1)如图1,AB=1,点E是AB的中点,求BD的长;
(2)点E是AB边上任意一点(不与AB边的中点和端点重合),依题意,将图2补全,判断AE与BD间的数量关系并证明;
(3)点E不在线段AB上,请在图3中画出符合条件的一个图形.

▼优质解答
答案和解析
(1)∵△ABC是等边三角形,点E是AB的中点,
∴∠BCE=
∠ACB=30°,
∵ED=EC,
∴∠D=∠BCE=30°,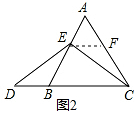
∵∠ABC=∠D+∠DEB=60°,
∴∠DEB=∠D=30°,
∴BD=BE=
AB=
;
(2)DB=AE成立;理由如下:
如图2,过点E作EF∥BC,交AC于F,则∠AEF=∠ABC,∠AFE=∠ACB,∠CEF=∠ECD,
∵∠A=∠ABC=∠ACB=60°,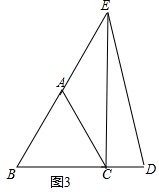
∴∠A=∠AEF=∠AFE=60°,
∠DBE=120°,
∴△AEF是等边三角形,∴AE=EF,∠EFC=120°,
∴BE=CF,∠DBE=∠EFC,
∵ED=EC,
∴∠D=∠ECD,
∴∠D=∠CEF,
在△DBE和△EFC中,
,
∴△DBE≌△EFC(AAS),
∴DB=EF,
∴AE=DB;
(3)如图3所示.
∴∠BCE=
| 1 |
| 2 |
∵ED=EC,
∴∠D=∠BCE=30°,

∵∠ABC=∠D+∠DEB=60°,
∴∠DEB=∠D=30°,
∴BD=BE=
| 1 |
| 2 |
| 1 |
| 2 |
(2)DB=AE成立;理由如下:
如图2,过点E作EF∥BC,交AC于F,则∠AEF=∠ABC,∠AFE=∠ACB,∠CEF=∠ECD,
∵∠A=∠ABC=∠ACB=60°,

∴∠A=∠AEF=∠AFE=60°,
∠DBE=120°,
∴△AEF是等边三角形,∴AE=EF,∠EFC=120°,
∴BE=CF,∠DBE=∠EFC,
∵ED=EC,
∴∠D=∠ECD,
∴∠D=∠CEF,
在△DBE和△EFC中,
|
∴△DBE≌△EFC(AAS),
∴DB=EF,
∴AE=DB;
(3)如图3所示.
看了 在等边三角形ABC中,E为直...的网友还看了以下:
压力容器的主要接头形式是()接头。A.对接B.搭接C.角接D.T形 2020-05-31 …
铜及铜合金焊接时,为获得成形均匀的焊缝,应采用()接头。A.搭接B.T形C.角接D.对接 2020-05-31 …
各位大虾··帮忙解小小的题—-—在Rt三角形ABC中,角C=90°,角A=30°,BC=2cm,则 2020-06-06 …
设角B角C的角平分线为y=1和x+y+1=0,设顶点A(-1,1),求直线BC的方程在三角形ABC 2020-07-30 …
1:如图直线AB,CD相交于点O,EO垂直于AB,O点为垂点,OF平角AOC且角EOC=2/5角A 2020-07-30 …
四边形ABCD中.若角A+角C=角B+角D,那么ABCD是圆的内接四边形吗?要推理过程哦,谢谢!圆 2020-08-01 …
下列说法不同确的是()A60度的角和12度的角互位补角B35度的角和55度的角是互为余角C钝角的补 2020-08-02 …
下列命题中,假命题的是()A.同旁内角相等,两直线平行B.等腰三角形的两个底角相等C.同角(等角)的 2020-11-01 …
如图所示,图中箭头表示接好电路时的电流方向,A、B、C三处分别接有电源、电铃、电灯,则根据电流方向可 2020-11-03 …
下列说法错误的是()A.三角形的中线、高、角平分线都是线段B.任意三角形内角和都是180°C.三角形 2021-01-30 …