如图，在平面直角坐标系中，矩形OABC，OA=3，OC=6，将△ABC沿对角线AC翻折，使点B落在点B′处，AB′与y轴交于点D，则点D的坐标为（）A.（0，-92）B.（0，-94）C.（0，-72）D.（0，-74）

Question

如图，在平面直角坐标系中，矩形OABC，OA=3，OC=6，将△ABC沿对角线AC翻折，使点B落在点B′处，AB′与y轴交于点D，则点D的坐标为（　　）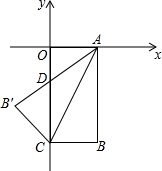

A. （0，-

(9)/(2)）

B. （0，-

(9)/(4)）

C. （0，-

(7)/(2)）

D. （0，-

(7)/(4)）

Answer 1

由折叠的性质可知，∠B′AC=∠BAC，
∵四边形OABC为矩形，
∴OC∥AB，
∴∠BAC=∠DCA，
∴∠B′AC=∠DCA，
∴AD=CD，
设OD=x，则DC=6-x，在Rt△AOD中，由勾股定理得，
OA²+OD²=AD²，
即9+x²=（6-x）²，
解得：x=(9)/(4)，
∴点D的坐标为：（0，-(9)/(4)），
故选：B．