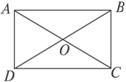
如下图已知四边形ABCD是矩形O是对角线AC与BD的交点.设点集M={ABCDO}向量的集合T={|PQ∈M且PQ不重合}.试求集合T的子集个数.
设点集M={A B C D O} 向量的集合T={ 
|P Q∈M 且P Q不重合}.试求集合T的子集个数.
解:以矩形ABCD的四个顶点及对角线交点这五个点中的任一点为起点 其他四点中的一点为终点的向量共有20个 但这20个向量中有些是相等的 只能作为一个元素.我们一一列举出来:
它们中共有12个向量各不相等 故集合T有12个元素 有2 12 个子集.
点评：要确定向量为元素的集合T有多少个子集 就需要弄清楚集合T中有多少个相异向量.在上述解题过程中 我们一定要根据集合元素的互异性 算出集合T中的元素个数为12 而不是20.
二次函数已知函数y=-ax2+bx+c（a≠0）图像过点P（-1,2）和Q（2,4）.证明：无论a 2020-05-13 …
概率加法公式加法公式,对于任意两事件A,B,有P（A并B)=P(A)+P(B)-P(AB)成立,假 2020-05-16 …
1.已知P={y|y=x平方－2x+3,0大于等于x小于等于3},Q={x|y=根号下x-a}.（ 2020-06-12 …
星期一之前)1.chat过去式2.两条直线相交有几个交点?3条直线相交最多有几个相交?4条直线相交 2020-07-17 …
p(aandb)p(banda)有区别么?统计学：公式：p(aandb)=p(a)*p(b/a)呢 2020-07-22 …
1、设p、q是两个数,规定：p△q=3×p-（p+q）÷2,求7△（2△4）2、如果1*5=1、设 2020-07-24 …
（2011•百色）我们知道：一个正整数p（p＞1）的正因数有两个：1和p，除此之外没有别的正因数， 2020-07-31 …
设集合P={x|x^2-x-2≥0},Q={y|y=1/2×x^2-1,x∈P}则P交Q= 2020-08-02 …
..关于正方形的经典问题甲乙两个质量相同的实心正方体分别放在水平地面上,它们对水平地面的压强关系是P 2020-11-29 …
对于下述命题p，写出“¬p”形式的命题，并判断“p”与“¬p”的真假：(1)p：91∈(A∩B)(其 2020-12-13 …