已知O是坐标原点，点A（﹣1，1），若点M（x，y）为平面区域，上的一个动点，则•的取值范围是（）A．[﹣1，0]B．[0，1]C．[0，2]D．[﹣1，2]

Question

已知O是坐标原点，点A（﹣1，1），若点M（x，y）为平面区域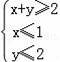，上的一个动点，则•的取值范围是（　　）

A．[﹣1，0] B．[0，1]   C．[0，2]   D．[﹣1，2]

Answer 1

C【考点】简单线性规划的应用；平面向量数量积的运算．

【专题】数形结合．

【分析】先画出满足约束条件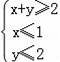的平面区域，求出平面区域的角点后，逐一代入•分析比较后，即可得到•的取值范围．

【解答】满足约束条件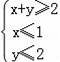的平面区域如下图所示：

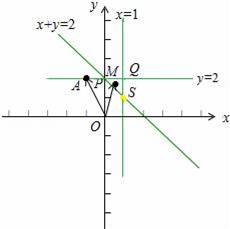
将平面区域的三个顶点坐标分别代入平面向量数量积公式

当x=1，y=1时， •=﹣1×1+1×1=0

当x=1，y=2时， •=﹣1×1+1×2=1

当x=0，y=2时， •=﹣1×0+1×2=2

故•和取值范围为[0，2]

解法二：

z=•=﹣x+y，即y=x+z

当经过P点（0，2）时在y轴上的截距最大，从而z最大，为2．

当经过S点（1，1）时在y轴上的截距最小，从而z最小，为0．

故•和取值范围为[0，2]

故选：C

【点评】本题考查的知识点是线性规划的简单应用，其中画出满足条件的平面区域，并将三个角点的坐标分别代入平面向量数量积公式，进而判断出结果是解答本题的关键．