早教吧作业答案频道 -->数学-->
如图,AB是O的直径,C是半圆的中点,连接CA,E是弦CD上一点,CE=CA,连接AD.(1)求证:AE平分∠BAD;(2)连接OE,若AB=10,AD=6,求OE的长.
题目详情
如图,AB是 O的直径,C是半圆的中点,连接CA,E是弦CD上一点,CE=CA,连接AD.
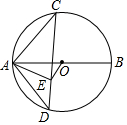
(1)求证:AE平分∠BAD;
(2)连接OE,若AB=10,AD=6,求OE的长.

(1)求证:AE平分∠BAD;
(2)连接OE,若AB=10,AD=6,求OE的长.
▼优质解答
答案和解析
(1)证明:∵C是半圆的中点,
∴
=
,
∴∠ADC=∠BAC,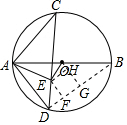
∵CE=CA,
∴∠CAE=∠CEA,又∠CEA=∠ADC+∠EAD,
∴∠BAE=∠DAE,即AE平分∠BAD;
(2) 连接BD,作EF⊥BD于D,OG⊥BD于G,EH⊥OG于H,
由勾股定理得,BD=
=8,
∵C是半圆的中点,
∴DC平分∠ADB,又AE平分∠BAD,
∴E是△ADB的内心,
∴EF=
=2,
∵∠CDB=45°,
∴DF=EF=2,
∵OG⊥BD,
∴DG=
BD=4,
∴FG=2,
∴EH=FG=2,
∵OG是△BAD的中位线,
∴OG=
AD=3,
∴OH=1,
∴OE=
=
.
∴
 |
| AC |
 |
| BC |
∴∠ADC=∠BAC,

∵CE=CA,
∴∠CAE=∠CEA,又∠CEA=∠ADC+∠EAD,
∴∠BAE=∠DAE,即AE平分∠BAD;
(2) 连接BD,作EF⊥BD于D,OG⊥BD于G,EH⊥OG于H,
由勾股定理得,BD=
| AB2-AD2 |
∵C是半圆的中点,
∴DC平分∠ADB,又AE平分∠BAD,
∴E是△ADB的内心,
∴EF=
| 6+8-10 |
| 2 |
∵∠CDB=45°,
∴DF=EF=2,
∵OG⊥BD,
∴DG=
| 1 |
| 2 |
∴FG=2,
∴EH=FG=2,
∵OG是△BAD的中位线,
∴OG=
| 1 |
| 2 |
∴OH=1,
∴OE=
| EH2+OH2 |
| 5 |
看了 如图,AB是O的直径,C是半...的网友还看了以下:
abcde是含有一种相同元素的五种物质,可发生如下转换a→bb→ca→cc→dd→e如果a是一种常 2020-06-12 …
已知CD是经过∠BCA的顶点C的一条直线,CA=CB,E,F分别是直线CD上的两点,且∠BEC=∠ 2020-06-12 …
如图,已知点B的坐标为(6,9),点A的坐标为(6,6),点P为⊙A上一动点,PB的延长线交⊙A于 2020-06-23 …
线性代数,求大神帮忙~设abc均为n阶矩阵,E为单位矩阵,若B=E+AB,C=A+CA,则B-C= 2020-06-24 …
如图,AB是O的直径,C是半圆的中点,连接CA,E是弦CD上一点,CE=CA,连接AD.(1)求证 2020-07-30 …
一次唱歌比赛,A.B.C.D.E,五位同学位于前五名,事后有人问他们的名次,他们是这样回答的A说B第 2020-10-31 …
一个简单化学推断ABCDE五种物质都含有钠元素A→CA→H2O→DA→空气中短期接触→BB→H2O→ 2020-11-06 …
已知CD是经过∠BCA的顶点C的一条直线,CA=CB,E、F分别是直线CD上的两点,且∠BEC=∠C 2020-11-27 …
如图是豆子生长过程的几个图片,不过次序已经打乱了,正确的顺序是a、e、b、d、ca、e、b、d、c( 2020-12-05 …
如图△ABC为等边三角形,直线a∥AB,D为直线BC上一点,∠ADE交直线a于点E,且∠ADE=60 2021-01-19 …