早教吧作业答案频道 -->数学-->
四边形ABCD中,点E、F、G、H分别为AB、BC、CD、DA边的中点,顺次连接各边中点得到的新四边形EFGH称为中点四边形.(1)我们知道:无论四边形ABCD怎样变化,它的中点四边形EFGH都是平行四边
题目详情
四边形ABCD中,点E、F、G、H分别为AB、BC、CD、DA边的中点,顺次连接各边中点得到的新四边形EFGH称为中点四边形.
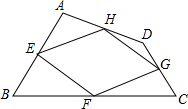
(1)我们知道:无论四边形ABCD怎样变化,它的中点四边形EFGH都是平行四边形.特殊的:
①当对角线AC=BD时,四边形ABCD的中点四边形为___形;
②当对角线AC⊥BD时,四边形ABCD的中点四边形是___形.
(2)如图:四边形ABCD中,已知∠B=∠C=60°,且BC=AB+CD,请利用(1)中的结论,判断四边形ABCD的中点四边形EFGH的形状并进行证明.

(1)我们知道:无论四边形ABCD怎样变化,它的中点四边形EFGH都是平行四边形.特殊的:
①当对角线AC=BD时,四边形ABCD的中点四边形为___形;
②当对角线AC⊥BD时,四边形ABCD的中点四边形是___形.
(2)如图:四边形ABCD中,已知∠B=∠C=60°,且BC=AB+CD,请利用(1)中的结论,判断四边形ABCD的中点四边形EFGH的形状并进行证明.
▼优质解答
答案和解析
(1)①连接AC、BD,
∵点E、F、G、H分别为AB、BC、CD、DA边的中点,
∴EH∥BD,FG∥BD,
∴EH∥FG,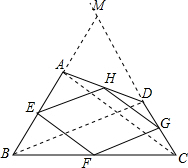
同理EF∥HG,
∴四边形EFGH都是平行四边形,
∵对角线AC=BD,
∴EH=EF,
∴四边形ABCD的中点四边形是菱形;
②当对角线AC⊥BD时,EF⊥EH,
∴四边形ABCD的中点四边形是矩形;
(2)四边形ABCD的中点四边形EFGH是菱形.理由如下:
分别延长BA、CD相交于点M,连接AC、BD,
∵∠ABC=∠BCD=60°,
∴△BCM是等边三角形,
∴MB=BC=CM,∠M=60°,
∵BC=AB+CD,
∴MA+AB=AB+CD=CD+DM
∴MA=CD,DM=AB,
在△ABC和△DMB中,
,
∴△ABC≌△DMB,
∴AC=DB,
∴四边形ABCD的对角线相等,中点四边形EFGH是菱形.
∵点E、F、G、H分别为AB、BC、CD、DA边的中点,
∴EH∥BD,FG∥BD,
∴EH∥FG,

同理EF∥HG,
∴四边形EFGH都是平行四边形,
∵对角线AC=BD,
∴EH=EF,
∴四边形ABCD的中点四边形是菱形;
②当对角线AC⊥BD时,EF⊥EH,
∴四边形ABCD的中点四边形是矩形;
(2)四边形ABCD的中点四边形EFGH是菱形.理由如下:
分别延长BA、CD相交于点M,连接AC、BD,
∵∠ABC=∠BCD=60°,
∴△BCM是等边三角形,
∴MB=BC=CM,∠M=60°,
∵BC=AB+CD,
∴MA+AB=AB+CD=CD+DM
∴MA=CD,DM=AB,
在△ABC和△DMB中,
|
∴△ABC≌△DMB,
∴AC=DB,
∴四边形ABCD的对角线相等,中点四边形EFGH是菱形.
看了 四边形ABCD中,点E、F、...的网友还看了以下:
什么是平行四边形知道的请回答 2020-05-14 …
不规则四边形知道四个点的坐标,怎样求面积? 2020-05-14 …
不规则四边形知道四个边长11m\12.7m\11.5m\20m求面积这是一块土地的数据 2020-05-14 …
平行四边形知道一边长和一对角线如何求另一边取值范围 2020-05-23 …
一个任意四边形知道四边的长度就可以知道面积记得是古希腊数学家海伦-凯乐给出了一个求任意四边形的面积 2020-06-02 …
一个平行四边形,知道底边上的高是2.4斜边上的高是2.3算四边形面积 2020-11-27 …
四边形知道底边90MM,内部可画5个相同大小的圆而且圆心都在对角线上,求四边形的高是多少?四边形有可 2020-11-27 …
百思不得其解CAD怎么在圆的外面画一个与圆相切的平行四边形?知道圆的直径20知道平行四边形的线长是4 2020-12-10 …
平行四边形知道两条高怎么求周长 2021-02-17 …
平行四边形知道面积求周长要公式 2021-02-17 …