早教吧作业答案频道 -->数学-->
如图,已知点A(m,m+1),B(m+3,m-1)(1)求线段AB的长;(2)若已知m=3,x轴上是否存在一点P,使得PA+PB的值最小?若存在,请求出点P的坐标,若不存在,请说明理由;(3)如果M为x轴上
题目详情
如图,已知点A(m,m+1),B(m+3,m-1)
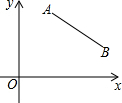
(1)求线段AB的长;
(2)若已知m=3,x轴上是否存在一点P,使得PA+PB的值最小?若存在,请求出点P的坐标,若不存在,请说明理由;
(3)如果M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.

(1)求线段AB的长;
(2)若已知m=3,x轴上是否存在一点P,使得PA+PB的值最小?若存在,请求出点P的坐标,若不存在,请说明理由;
(3)如果M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
▼优质解答
答案和解析
(1)∵点A(m,m+1),B(m+3,m-1),
∴AB=
=
=
,
(2)如图1,
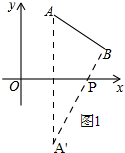
∵m=3,
∴A(3,4),B(6,5),
作出点A关于x轴的对称点A'(3,-4),
∴设直线A'B的解析式为y=kx+b,
∴
,
∴
∴直线A'B的解析式为y=3x-13,
令y=0,则3x-13=0,
∴x=
,
∴P(
,0);
(3)如图2,
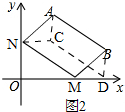
∵M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,
∴AB不可能是平行四边形的对角线,只能是平行四边形的一边,
∵A(m,m+1),B(m+3,m-1)
①点B平移到x轴上,
∴将线段AB向下平移(m-1)个单位,点B落在x轴上,
∴平移后点A的对应点C(m.(m+1)-(m-1)),即:C(m,2),
平移后点B的对应点D(m+3,0)
∵点N在y轴上,
∴N(0,2),
再将线段CD向左平移m单位,点C落在y轴上,
∴M((m+3)-m,0),即:M(3,0),
∴直线MN的解析式为y=-
x+2.
②点A平移到x轴上,
如图3,
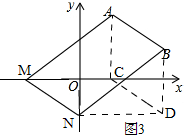
同①的方法得出直线MN的解析式为y=-
x-2.
即:直线MN的解析式为y=-
x+2或y=-
x-2.
∴AB=
| [(m+3)-m]2+[(m-1)-(m+1)]2 |
=
| 9+4 |
=
| 13 |
(2)如图1,

∵m=3,
∴A(3,4),B(6,5),
作出点A关于x轴的对称点A'(3,-4),
∴设直线A'B的解析式为y=kx+b,
∴
|
∴
|
∴直线A'B的解析式为y=3x-13,
令y=0,则3x-13=0,
∴x=
| 13 |
| 3 |
∴P(
| 13 |
| 3 |
(3)如图2,

∵M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,
∴AB不可能是平行四边形的对角线,只能是平行四边形的一边,
∵A(m,m+1),B(m+3,m-1)
①点B平移到x轴上,
∴将线段AB向下平移(m-1)个单位,点B落在x轴上,
∴平移后点A的对应点C(m.(m+1)-(m-1)),即:C(m,2),
平移后点B的对应点D(m+3,0)
∵点N在y轴上,
∴N(0,2),
再将线段CD向左平移m单位,点C落在y轴上,
∴M((m+3)-m,0),即:M(3,0),
∴直线MN的解析式为y=-
| 2 |
| 3 |
②点A平移到x轴上,
如图3,

同①的方法得出直线MN的解析式为y=-
| 2 |
| 3 |
即:直线MN的解析式为y=-
| 2 |
| 3 |
| 2 |
| 3 |
看了 如图,已知点A(m,m+1)...的网友还看了以下:
已知二次函数两点坐标2,-1-1,-1怎么求对称轴 2020-05-14 …
急求..用123456组成不重复的组合求结果,例如1-2-3-4-5-66-?-?-?-?-55- 2020-06-04 …
求出(2+1)(2^+1)(2^4+1)(2^8+1)……(2^64+1)的过程要具体 2020-06-07 …
A坐标1/2,2,B坐标2,1/2,P坐标x,0,在X正半轴上运动,当AP与BP差最大时,P坐标 2020-06-14 …
已知ABC中,点A,B的坐标分别为(-√2,0)(√2,0)点C在X轴上方若点C坐标(√2,1), 2020-06-21 …
12岁男生的标准身高是153cm,12岁女生的标准身高是155cm.小勇和小梅今年都是12岁.小勇 2020-07-18 …
在直角坐标内,A的坐标(2,1),点B为x轴上一点,圆A与圆B只有一个公共点,圆A与圆B的半径长为 2020-07-29 …
如题:条件充分性判断:曲线ax^2+by^2=1通过四个定点.(1)a+b=1;(2)a+b=2答 2020-07-31 …
知道直线向量的坐标,怎么求它的斜率?请告诉具体的公式,好像有个公式,就是有题:已知向量坐标(2,- 2020-07-31 …
一个数学问题骰子问题。一个骰子,先后两次投掷。例如出现2.1和1.2的结果,本质到底是因为这是两种投 2020-12-30 …