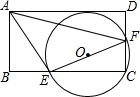
如图，矩形ABCD中，E为BC上一点，F为CD上一点，已知∠AEF=90°，AEEF=34，△ECF的外接圆与AD相切，则tan∠DAF=．

Question

如图，矩形ABCD中，E为BC上一点，F为CD上一点，已知∠AEF=90°， (AE)/(EF)= (3)/(4)，△ECF的外接圆与AD相切，则tan∠DAF=___．

Answer 1

设 O与直线AD相切于点M，连接MO，延长MO交BC于点N，
设AE=AM=3k，AB=3a，
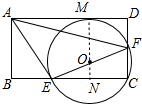∵∠AEF=90°，
∴∠AEB+∠FEC=90°，∠FEC+∠EFC=90°，
∴∠AEB=∠EFC，
∵∠C=∠B=90°，
∴△ABE∽△ECF，
∴(AB)/(EC)=(AE)/(EF)=(3)/(4)，
∴EC=4a，
∵OM⊥AD．AD∥BC，
∴ON⊥BC，
∴NE=NC=DM=2a，
∴BE=3k+2a-4a=3k-2a，
在RT△ABE中，∵AE²=AB²+BE²，
∴9k²=9a²+（3k-2a）²，
∴k=(13)/(12)a，
∴AM=(13)/(4)a，
∵DM²=DF•DC，
∴DF=(4)/(3)a，
∴tan∠ADF=(DF)/(AD)=((4)/(3)a)/((21)/(4)a)=(16)/(63)．
故答案为(16)/(63)．