在平面直角坐标系中，点A（-5，0），以OA为直径在第二象限内作半圆C，点B是该半圆周上一动点，连接OB、AB，作点A关于点B的对称点D，过点D作x轴垂线，分别交直线OB、x轴于点E、F，点F为垂

Question

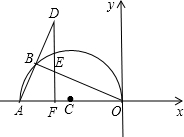
在平面直角坐标系中，点A（-5，0），以OA为直径在第二象限内作半圆C，点B是该半圆周上一动点，连接OB、AB，作点A关于点B的对称点D，过点D作x轴垂线，分别交直线OB、x轴于点E、F，点F为垂足，当DF=4时，线段EF=___．

Answer 1

连接OD，如图所示．

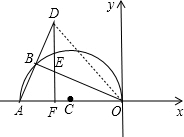
∵点A、点D关于B点对称，
∴OD=OA=5．
在Rt△ODF中，OD=5，DF=4，∠DFO=90°，
∴OF=√(OD2-DF2)=3，
∴AF=OA-OF=2．
∵AO为 C的直径，
∴∠ABO=90°，
∴∠DBE=90°=∠DFA，
又∵∠BDE=∠FDA，
∴△BDE∽△FDA，
∴(DE)/(DA)=(DB)/(DF)．
在Rt△ADF中，AF=2，DF=4，∠AFD=90°，
∴AD=√(DF2+AF2)=2√(5)．
∵OA=OD，且OB⊥AD，
∴AB=DB=(1)/(2)AD=√(5)，
∴DE=(DB•DA)/(DF)=(5)/(2)，
∴EF=DF-DE=(3)/(2)．
故答案为：(3)/(2)．