如图，在反比例函数y=-2x的图象上有一动点A，连接AO并延长交图象的另一支于点B，在第一象限内有一点C，满足AC=BC，当点A运动时，点C始终在函数y=kx的图象上运动．若tan∠CAB=2，则k的值为（

Question

如图，在反比例函数y=-

(2)/(x)的图象上有一动点A，连接AO并延长交图象的另一支于点B，在第一象限内有一点C，满足AC=BC，当点A运动时，点C始终在函数y=(k)/(x)的图象上运动．若tan∠CAB=2，则k的值为（　　）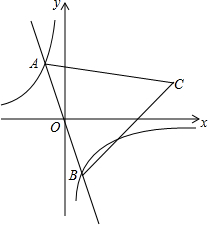

A. 2

B. 4

C. 6

D. 8

Answer 1

连接OC，过点A作AE⊥y轴于点E，过点C作CF⊥x轴于点F，如图所示．

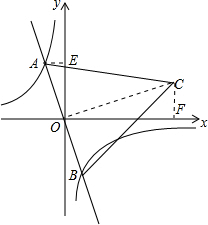
由直线AB与反比例函数y=(2)/(x)的对称性可知A、B点关于O点对称，
∴AO=BO．
又∵AC=BC，
∴CO⊥AB．
∵∠AOE+∠EOC=90°，∠EOC+∠COF=90°，
∴∠AOE=∠COF，
又∵∠AEO=90°，∠CFO=90°，
∴△AOE∽△COF，
∴(AE)/(CF)=(OE)/(OF)=(AO)/(CO)．
∵tan∠CAB=(OC)/(AO)=2，
∴CF=2AE，OF=2OE．
又∵AE•OE=|-2|=2，CF•OF=|k|，
∴k=±8．
∵点C在第一象限，
∴k=8．
故选D．