如图，在平面直角坐标系中，O为坐标原点，△ABO的边AB垂直于x轴，垂足为点B，反比例函数y=kx（x>0）的图象经过AO上的点C，且OCOA=23，与AB相交于点D，OB=6，AD=52，（1）求点C的横坐标；（2

Question

如图，在平面直角坐标系中，O为坐标原点，△ABO的边AB垂直于x轴，垂足为点B，反比例函数y=(k)/(x)（x>0）的图象经过AO上的点C，且(OC)/(OA)=(2)/(3)，与AB相交于点D，OB=6，AD=(5)/(2)，

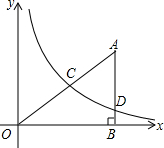
（1）求点C的横坐标；
（2）求反比例函数y=(k)/(x)的解析式；
（3）求经过C、D两点的一次函数解析式．

Answer 1

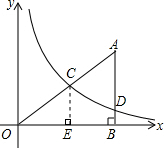
（1）如图，过点C作CE⊥x轴于点E，
∵AB⊥x轴，
∴CE∥AB，
∴(OE)/(OB)=(OC)/(OA)．
又∵(OC)/(OA)=(2)/(3)，OB=6，
∴(OE)/(6)=(2)/(3)，则OE=4，
∴点C的横坐标是4；

（2）设点D的坐标为（6，m）（m>0），则点A的坐标为（6，(5)/(2)+m），
∵点C的坐标为（4，(5)/(3)+(2)/(3)m）
∵点C、点D均在反比例函数y=(k)/(x)（x>0）的函数图象上，
∴6m=4×（(5)/(3)+(2)/(3)m），
解得：m=2．
故k=12
∴反比例函数的解析式为y=(12)/(x)．

（3）∵m=2，
∴点C的坐标为（4，3），点D的坐标为（6，2）．
设经过点C、D的一次函数的解析式为y=ax+b，
则有

4a+b=3

6a+b=2

，
解得：

a=-(1)/(2)

b=5

．
∴经过C、D两点的一次函数解析式为y=-(1)/(2)x+5．