已知正四面体ABCD的棱长为1，如果一高为36的长方体能在该正四面体内任意转动，则该长方体的长和宽形成的长方形面积的最大值为（）A.13B.16C.112D.124

Question

已知正四面体ABCD的棱长为1，如果一高为

(√(3))/(6)的长方体能在该正四面体内任意转动，则该长方体的长和宽形成的长方形面积的最大值为（　　）

A.

(1)/(3)

B.

(1)/(6)

C.

(1)/(12)

D.

(1)/(24)

Answer 1

设正四面体S-ABCD如图所示．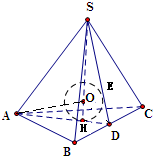
可得它的内切球的球心0必定在高线SH上，
延长AH交BC于点D，则D为BC的中点，连接SD，
则内切球切SD于点E，连接AO．
∵H是正三角形ABC的中心，
∴AH：HD=2：1，
∵Rt△0AH∽Rt△DSH，
∴(OA)/(OH)=(DS)/(DH)=3，可得OA=30H=S0
因此，SH=4OH，可得内切球的半径R=OH=(1)/(4)SH．
∵正四面体棱长为1，
∴Rt△SHD中，SD=√(SH2+HD2)=，√((4R)2+((1)/(3)×(√(3))/(2))2)=(√(3))/(2)，解得R²=(1)/(24)．
要满足一高为(√(3))/(6)的长方体能在该正四面体内任意转动，
则长方体的对角线长不超过正四面体的内切球的直径，
设该长方体的长和宽分别为x，y，
该长方体的长和宽形成的长方形面积为S．
∴4R²≥((√(3))/(6))2+x²+y²，
∴x²+y²≤(1)/(12)，
∴S=xy≤(x2+y2)/(2)=(1)/(24)．
故选：D．