早教吧作业答案频道 -->数学-->
设x3+ax+b=0,其中a,b均为实数,下列条件中,使得该三次方程仅有一个实根的是(写出所有正确条件的编号)①a=-3,b=-3.②a=-3,b=2.③a=-3,b>2.④a=0,b=2.⑤a=1,b=2.
题目详情
设x3+ax+b=0,其中a,b均为实数,下列条件中,使得该三次方程仅有一个实根的是___(写出所有正确条件的编号)
①a=-3,b=-3.②a=-3,b=2.③a=-3,b>2.④a=0,b=2.⑤a=1,b=2.
①a=-3,b=-3.②a=-3,b=2.③a=-3,b>2.④a=0,b=2.⑤a=1,b=2.
▼优质解答
答案和解析
设f(x)=x3+ax+b,f'(x)=3x2+a,
①a=-3,b=-3时,令f'(x)=3x2-3=0,解得x=±1,x=1时f(1)=-5,f(-1)=-1;
并且x>1或者x<-1时f'(x)>0,
所以f(x)在(-∞,-1)和(1,+∞)都是增函数,
所以函数图象与x轴只有一个交点,故x3+ax+b=0仅有一个实根;如图
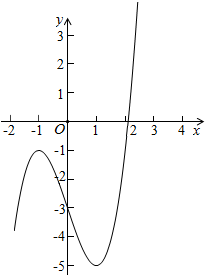
②a=-3,b=2时,令f'(x)=3x2-3=0,解得x=±1,x=1时f(1)=0,f(-1)=4;如图
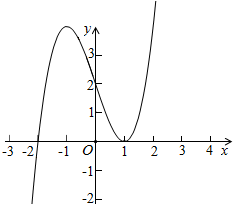
③a=-3,b>2时,函数f(x)=x3-3x+b,f(1)=-2+b>0,函数图象形状如图②,所以方程x3+ax+b=0只有一个根;
④a=0,b=2时,函数f(x)=x3+2,f'(x)=3x2≥0恒成立,故原函数在R上是增函数;故方程方程x3+ax+b=0只有一个根;
⑤a=1,b=2时,函数f(x)=x3+x+2,f'(x)=3x2+1>0恒成立,故原函数在R上是增函数;故方程方程x3+ax+b=0只有一个根;
综上满足使得该三次方程仅有一个实根的是①③④⑤.
故答案为:①③④⑤.
①a=-3,b=-3时,令f'(x)=3x2-3=0,解得x=±1,x=1时f(1)=-5,f(-1)=-1;
并且x>1或者x<-1时f'(x)>0,
所以f(x)在(-∞,-1)和(1,+∞)都是增函数,
所以函数图象与x轴只有一个交点,故x3+ax+b=0仅有一个实根;如图
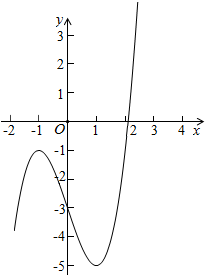
②a=-3,b=2时,令f'(x)=3x2-3=0,解得x=±1,x=1时f(1)=0,f(-1)=4;如图
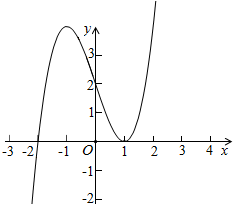
③a=-3,b>2时,函数f(x)=x3-3x+b,f(1)=-2+b>0,函数图象形状如图②,所以方程x3+ax+b=0只有一个根;
④a=0,b=2时,函数f(x)=x3+2,f'(x)=3x2≥0恒成立,故原函数在R上是增函数;故方程方程x3+ax+b=0只有一个根;
⑤a=1,b=2时,函数f(x)=x3+x+2,f'(x)=3x2+1>0恒成立,故原函数在R上是增函数;故方程方程x3+ax+b=0只有一个根;
综上满足使得该三次方程仅有一个实根的是①③④⑤.
故答案为:①③④⑤.
看了 设x3+ax+b=0,其中a...的网友还看了以下:
已知关于x的方程(x/2)-x=-a的解是方程(2/3)x-(1/12)(x+116)=(1/2)x 2020-03-30 …
利用完全平方式计算:1.如果x^2+ax+4是一个完全平方式,则a等于?2.若代数式x^2-6x+b 2020-03-31 …
因式分解,-4x^3+16x^2-26xmn(m-n)-m(n-m)5(x-y)^3+10(y-x 2020-04-08 …
若关于x的方程(x-b)/a=2-(x-a)/b有唯一解,则字母a、b应当满足的条件是多少b(x- 2020-05-13 …
已知圆C1:(x-a)2+(y+2)2=4与圆C2:(x+b)2+(y+2)2=1相外切,则ab的 2020-05-13 …
运用公式计算 (a+b)(a-b)(a2-b2)运用公式计算---过程!1.(a+b)(a-b)( 2020-05-16 …
若函数f(x)在x=a处的导函数值为A(aA不等于0),函数F(x)=f(x)-A^2x^2满足F 2020-05-21 …
(-x/y)的2次方*(-y的2次方/x)/(-xy的4次方)(a的2次方b/c的3次方)/的2次 2020-06-04 …
帮我将这个二元一次方程化为一般形式!x的2次方-(2a-b)x+a的2次方-ab-2b的2次方=0 2020-06-06 …
求证几个函数对称定理!50待加.1.函数f(x)定义域为R.求证y=f(x-m)与y=f(m-x) 2020-06-06 …