早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax-3a与x轴交于A、B两点,与y轴交于点C,BO=CO.(1)求抛物线的解析式;(2)点P是第一象限抛物线上的一动点,连接AP,交y轴于点D,
题目详情
如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax-3a与x轴交于A、B两点,与y轴交于点C,BO=CO.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一动点,连接AP,交y轴于点D,连接CP,设P点横坐标为t,△CDP的面积为S,求S与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点P作PE⊥x轴于点E,连接PB,过点A作AF⊥PB于点F,交线段PE于点G,若点H在x轴负半轴上,PH=2GE,点M(0,m)在y轴正半轴上,连接PM、PH,∠HPM=2∠BHP,PH=2PM,求m的值.

(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一动点,连接AP,交y轴于点D,连接CP,设P点横坐标为t,△CDP的面积为S,求S与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点P作PE⊥x轴于点E,连接PB,过点A作AF⊥PB于点F,交线段PE于点G,若点H在x轴负半轴上,PH=2GE,点M(0,m)在y轴正半轴上,连接PM、PH,∠HPM=2∠BHP,PH=2PM,求m的值.
▼优质解答
答案和解析
(1)当ax2-2ax-3a=0时,解得x=3或-1,
∴A(-1,0),B(3,0),
∴OA=1,OB=3,
∴OC=OB=3,
∴-3a=3,
∴a=-1,
∴y=-x2+2x+3.
(2)如图1中,作PE⊥x轴于E,PK⊥y轴于K.
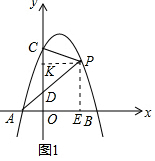
∵点P在第一象限,横坐标为t,
∴P(t,-t2+2t+3),
∵∠PKO=∠COB=∠PEO=90°,
∴四边形KPEO是矩形,
∴PK=OE=t,PE=OK,
∴PE=-t2+2t+3,AE=t+1,
∵∠PAE=∠DAO,
∴tan∠PAE=tan∠DAO,
∴
=
,
∴
=
,
∴OD=3-t,
∴CD=3-OD=t,
∴S=
PK•CD=
t2.
(3)设PH交y轴于点N.
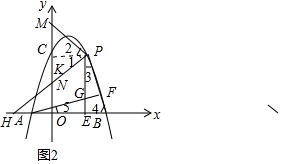
∵∠PKO=∠PKM=∠HON=90°,
∴PK∥x轴,
∴∠1=∠PHB,
∵∠MPH=2∠PHB,
∴MPH=2∠1,即∠1=∠2,
∵∠PKM=∠PKN,PK=PK,
∴△PKM≌△PKN,
∴PM=PN,MK=NK,
∵PH=2PM,
∴PN=HN,
∵∠HON=∠PKN,∠1=∠BHP,
∴△HON≌△PKN,
∴PK=HO,KN=ON,
∵AF⊥PB,
∴∠AFB=90°,
∴∠3+∠4=90°,
∵∠PEB=90°,
∴∠4+∠5=90°,
∴∠3=∠5,
∴tan∠3=tan∠5,
∴
=
,∵BE=OB-OE=3-t,
∴
=
,
∴GE=1,
∴OH=2EG=2,
∴PK=2,PE=3,
∴OK=3=OC,
∴点K与点C重合,
∴KN=
,
∴OM=3KN=
,即m=
∴A(-1,0),B(3,0),
∴OA=1,OB=3,
∴OC=OB=3,
∴-3a=3,
∴a=-1,
∴y=-x2+2x+3.
(2)如图1中,作PE⊥x轴于E,PK⊥y轴于K.

∵点P在第一象限,横坐标为t,
∴P(t,-t2+2t+3),
∵∠PKO=∠COB=∠PEO=90°,
∴四边形KPEO是矩形,
∴PK=OE=t,PE=OK,
∴PE=-t2+2t+3,AE=t+1,
∵∠PAE=∠DAO,
∴tan∠PAE=tan∠DAO,
∴
| PE |
| AE |
| DO |
| AO |
∴
| -t2+2t+3 |
| t+1 |
| OD |
| 1 |
∴OD=3-t,
∴CD=3-OD=t,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
(3)设PH交y轴于点N.

∵∠PKO=∠PKM=∠HON=90°,
∴PK∥x轴,
∴∠1=∠PHB,
∵∠MPH=2∠PHB,
∴MPH=2∠1,即∠1=∠2,
∵∠PKM=∠PKN,PK=PK,
∴△PKM≌△PKN,
∴PM=PN,MK=NK,
∵PH=2PM,
∴PN=HN,
∵∠HON=∠PKN,∠1=∠BHP,
∴△HON≌△PKN,
∴PK=HO,KN=ON,
∵AF⊥PB,
∴∠AFB=90°,
∴∠3+∠4=90°,
∵∠PEB=90°,
∴∠4+∠5=90°,
∴∠3=∠5,
∴tan∠3=tan∠5,
∴
| GE |
| AE |
| BE |
| PE |
∴
| GE |
| t+1 |
| 3-t |
| -t2+2t+3 |
∴GE=1,
∴OH=2EG=2,
∴PK=2,PE=3,
∴OK=3=OC,
∴点K与点C重合,
∴KN=
| 3 |
| 2 |
∴OM=3KN=
| 9 |
| 2 |
| 9 |
| 2 |
看了 如图,在平面直角坐标系中,O...的网友还看了以下:
在事件2中: (1)在布线中,施工人员的做法可能会导致线缆的哪两项指标超标? (2)总监理工程师签发 2020-05-26 …
在事件2中:(1)监理工程师应如何协调处理?(2)合同的变更和解除,会影响当事人要求赔偿损失的权利吗 2020-05-26 …
(3x-6)^2-(x+m)^2中1次项系数是-54 2020-06-06 …
三个数的比中谁是前项与后项在1:2中1是前项,2是后项.那么,在1:2:3中谁是前项和后项,这三个 2020-07-11 …
1.如图,点O是等边△ABC内一点,AO=√3,BO=√2,CO=1,将△BOCa绕点C按顺时针方 2020-08-01 …
如图,在图1、图2,在3×3的方格内填写了一些代数式与数字.(1)图1中各行各列及对角线上三个数字 2020-08-01 …
1,匀加速运动f=1/2at^2中1/2是怎样推来的?2,如果速度是df/dt,那么加速度a=d^2 2020-11-01 …
我的暑假作业多吗?有语数英各一本暑假作业一本47页,英语星单词抄5中1,其他的抄2中1.六个单元的对 2020-11-20 …
(10分)下图1表示人体内苯丙氨酸与酪氨酸的代谢途径,图中数字分别代表三种酶。图2表示苯丙酮尿症、尿 2020-11-24 …
图1表示与缩手反射相关的结构,图2、图3是图1中某一结构放大后的结构模式图.请分析回答:(1)图1中 2020-12-21 …