早教吧作业答案频道 -->数学-->
如图,二次函数y=mx2+(m2-m)x-2m+1的图象与x轴交于点A、B,与y轴交于点C,顶点D的横坐标为1.(1)求二次函数的表达式及A、B的坐标;(2)若P(0,t)(t<-1)是y轴上一点,Q(-5,0),将
题目详情
如图,二次函数y=mx2+(m2-m)x-2m+1的图象与x轴交于点A、B,与y轴交于点C,顶点D的横坐标为1.
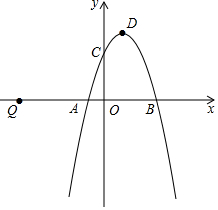
(1)求二次函数的表达式及A、B的坐标;
(2)若P(0,t)(t<-1)是y轴上一点,Q(-5,0),将点Q绕着点P顺时针方向旋转90°得到点E.当点E恰好在该二次函数的图象上时,求t的值;
(3)在(2)的条件下,连接AD、AE.若M是该二次函数图象上一点,且∠DAE=∠MCB,求点M的坐标.

(1)求二次函数的表达式及A、B的坐标;
(2)若P(0,t)(t<-1)是y轴上一点,Q(-5,0),将点Q绕着点P顺时针方向旋转90°得到点E.当点E恰好在该二次函数的图象上时,求t的值;
(3)在(2)的条件下,连接AD、AE.若M是该二次函数图象上一点,且∠DAE=∠MCB,求点M的坐标.
▼优质解答
答案和解析
(1)∵抛物线的顶点坐标的横坐标为1,
∴-
=1,
解得,m1=-1,m2=0(舍去)
∴二次函数的表达式为y=-x2+2x+3,
当y=0时,-x2+2x+3=0,
解得,x1=-1,x2=3,
∴A(-1,0),B(3,0),
(2)如图1,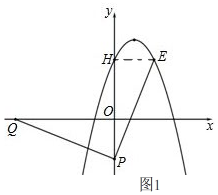 过点E作EH⊥y轴于点H,
过点E作EH⊥y轴于点H,
∵∠PQO+∠OPQ=90°,∠OPQ+∠HPE=90°,
∴∠HPE=∠PQO,
由旋转知,PQ=PE,
在△EPH和△PQO中,
,
∴△EPH≌△PQO,
∴EH=OP=-t,HP=OQ=5
∴E(-t,5+t)
当点E恰好在该二次函数的图象上时,有5+t=-t2-2t+3
解得t1=-2,t2=-1(由于t<-1所以舍去),
(3)设点M(a,-a2+2a+3)
①若点M在x轴上方,
如图2,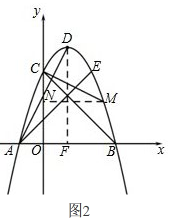 过点M作MN⊥y轴于点N,
过点M作MN⊥y轴于点N,
过点D作DF⊥x轴于点F.
∵∠EAB=∠OCB=45°,∠DAE=∠MCB
∴∠MCN=∠DAF
∴△MCN∽△DAF,
∴
=
,即
=
∴a1=
,a2=0(舍去)
∴M(
,
),
②若点M在x轴下方,
如图3,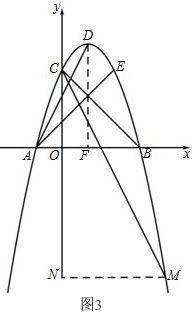 过点M作MN⊥y轴于点N,
过点M作MN⊥y轴于点N,
过点D作DF⊥x轴于点F.
∵∠EAB=∠OCB=45°,∠DAE=∠MCB
∴∠MCN=∠ADF
∴△MCN∽△ADF
∴
=
,即
=
∴a1=4,a2=0(舍去)
∴M(4,-5)
综上所述,M(
,
)或M(4,-5).
∴-
| m2-m |
| 2m |
解得,m1=-1,m2=0(舍去)
∴二次函数的表达式为y=-x2+2x+3,
当y=0时,-x2+2x+3=0,
解得,x1=-1,x2=3,
∴A(-1,0),B(3,0),
(2)如图1,
 过点E作EH⊥y轴于点H,
过点E作EH⊥y轴于点H,∵∠PQO+∠OPQ=90°,∠OPQ+∠HPE=90°,
∴∠HPE=∠PQO,
由旋转知,PQ=PE,
在△EPH和△PQO中,
|
∴△EPH≌△PQO,
∴EH=OP=-t,HP=OQ=5
∴E(-t,5+t)
当点E恰好在该二次函数的图象上时,有5+t=-t2-2t+3
解得t1=-2,t2=-1(由于t<-1所以舍去),
(3)设点M(a,-a2+2a+3)
①若点M在x轴上方,
如图2,
 过点M作MN⊥y轴于点N,
过点M作MN⊥y轴于点N,过点D作DF⊥x轴于点F.
∵∠EAB=∠OCB=45°,∠DAE=∠MCB
∴∠MCN=∠DAF
∴△MCN∽△DAF,
∴
| MN |
| DF |
| NC |
| FA |
| a |
| 4 |
| a2-2a |
| 2 |
∴a1=
| 5 |
| 2 |
∴M(
| 5 |
| 2 |
| 7 |
| 4 |
②若点M在x轴下方,
如图3,
 过点M作MN⊥y轴于点N,
过点M作MN⊥y轴于点N,过点D作DF⊥x轴于点F.
∵∠EAB=∠OCB=45°,∠DAE=∠MCB
∴∠MCN=∠ADF
∴△MCN∽△ADF
∴
| MN |
| AF |
| NC |
| DF |
| a |
| 2 |
| a2-2a |
| 4 |
∴a1=4,a2=0(舍去)
∴M(4,-5)
综上所述,M(
| 5 |
| 2 |
| 7 |
| 4 |
看了 如图,二次函数y=mx2+(...的网友还看了以下:
已知一次函数y1=kx+b(k≠0)的图象经过(2,0),(4,1)两点,二次函数y2=x2-2a 2020-05-16 …
已知二次函数的图象过坐标原点,它的顶点坐标是(1,-2),求这个二次函数的关系式. 2020-05-16 …
如图,在平面直角坐标系中,二次函数y=-14x2+bx+c的图象与坐标轴交于A、B、C三点,其中点 2020-06-08 …
如果点P(x,y)的坐标满足x的平方-y的平方=0,那么点P的位置是()A.在第一、三象限坐标轴夹 2020-07-21 …
初二坐标+函数题(求过程27.如图,点P是一个反比例函数与正比例函数的图象的交点,PQ垂直于x轴, 2020-07-22 …
画坐标的本子叫做什么就是画什么第一象限,第二象限,第三象限,第四象限坐标的那个本子,叫什么来着?就 2020-07-28 …
二次函数y=12x2−2x−2的图象在坐标平面内绕顶点旋转180°,再向左平移3个单位,向上平移5 2020-08-02 …
想问几道关于初三数学的问题(二次函数)1.为什么,在求二次函数的解析式时,如果设的解析式是二次函数的 2020-11-07 …
已知二次函数。(1)求函数图象的顶点坐标和对称轴;(2)求函数图象与坐标轴的交点坐标;(3)画出此函 2021-01-15 …
已知二次函数y=x2-2x-3(1)求函数图象的顶点坐标和对称轴;(2)求函数图象与坐标轴的交点坐标 2021-01-15 …