如图，在平面直角坐标系xOy中，把抛物线C1：y=-x2沿x轴翻折，再平移得到抛物线C2，恰好经过点A（-3，0）、B（1，0），抛物线C2与y轴交于点C，抛物线C1：y=-x2与抛物线C2的对称轴交于D点．（1

Question

如图，在平面直角坐标系xOy中，把抛物线C₁：y=-x²沿x轴翻折，再平移得到抛物线C₂，恰好经过点A（-3，0）、B（1，0），抛物线C₂与y轴交于点C，抛物线C₁：y=-x²与抛物线C₂的对称轴交于D点．

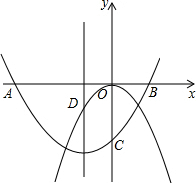
（1）求抛物线C₂的表达式．
（2）在抛物线C₂的对称轴上是否存在一点M，使得以M、O、D为顶点的三角形与△BOD相似？若存在，求点M坐标；若不存在，说明理由．

Answer 1

（1）设抛物线C₂的表达式为y=a（x+3）（x-1）．
∵由翻折可平移的性质可知抛物线C₁与抛物线C₂的开口大小相同，方向相反，
∴抛物线C₂的二次项系数与抛物线C₁的二次项系数互为相反数．
∴抛物线C₂的二次项系数为1，即a=1．
∴抛物线C₂的表达式为y=（x+3）（x-1），整理得：y=x²+2x-3．
（2）如图所示：

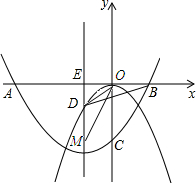
∵抛物线C₂的对称轴x=-(b)/(2a)=-1，
∴点E的坐标为（-1，0）．
∵将x=-1代入y=-x²得：y=-1，
∴D（-1，-1）．
∴OE=DE=1．
∴△OED为等腰直角三角形．
∴OD=√(2)，∠EOD=∠EDO=45°．
∴∠DOB=135°．
在Rt△EDB中，DB=√(EB2+ED2)=√(5)．
∵∠DOB=135°，
∴M点只能在D点下方．
∵∠BDM=∠BOD=135°，
∴当(MD)/(OD)=(OD)/(OB)或(MD)/(OD)=(OB)/(OD)时，以M、O、D为顶点的三角形与△BOD相似．
∵当(MD)/(OD)=(OD)/(OB)时，(MD)/(√(2))=(√(2))/(1)，解得：MD=2．
∴点M的坐标为（-1，-3）．
∵当(MD)/(OD)=(OB)/(OD)时，(MD)/(√(2))=(1)/(作业帮用户2017-04-03扫描下载二维码©2019 作业帮 联系方式：[e-mail]作业帮协议)