早教吧作业答案频道 -->数学-->
已知抛物线y=ax2+bx+c(a<0)经过点A(-3,0)、B(1,0),且与y轴交于点C,设抛物线的顶点为D.(1)求点C、D的坐标(用含a的式子表示);(2)当a变化时,△ACD能否为直角三角形?若能
题目详情
已知抛物线y=ax2+bx+c(a<0)经过点A(-3,0)、B(1,0),且与y轴交于点C,设抛物线的顶点为D.
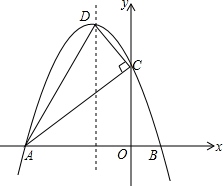
(1)求点C、D的坐标(用含a的式子表示);
(2)当a变化时,△ACD能否为直角三角形?若能?求出所有符合条件的a的值;若不能,请说明理由.

(1)求点C、D的坐标(用含a的式子表示);
(2)当a变化时,△ACD能否为直角三角形?若能?求出所有符合条件的a的值;若不能,请说明理由.
▼优质解答
答案和解析
(1)∵抛物线y=ax2+bx+c(a<0)经过点A(-3,0)、B(1,0),
∴可以假设抛物线为y=a(x+3)(x-1)=a(x2+2x-3)=a(x+1)2-4a,
∴顶点D(-1,-4a),
令x=0得y=-3a,得点C(0,-3a),
∴点C(0,-3a),点D(-1,-4a).
(2)①若∠ADC=90°则有AC2=AD2+DC2,
∴9+9a2=4+16a2+1+a2,
∴a2=
,
∵a<0,
∴a=-
.
②若∠DCA=90°则有AD2=AC2+CD2,
∴4+16a2=9+9a2+1+a2,
∴a2=1,
∵a<0,
∴a=-1,
综上所述a=-1或-
.
∴可以假设抛物线为y=a(x+3)(x-1)=a(x2+2x-3)=a(x+1)2-4a,
∴顶点D(-1,-4a),
令x=0得y=-3a,得点C(0,-3a),
∴点C(0,-3a),点D(-1,-4a).
(2)①若∠ADC=90°则有AC2=AD2+DC2,
∴9+9a2=4+16a2+1+a2,
∴a2=
| 1 |
| 2 |
∵a<0,
∴a=-
| ||
| 2 |
②若∠DCA=90°则有AD2=AC2+CD2,
∴4+16a2=9+9a2+1+a2,
∴a2=1,
∵a<0,
∴a=-1,
综上所述a=-1或-
| ||
| 2 |
看了 已知抛物线y=ax2+bx+...的网友还看了以下:
如图,抛物线y=-x^2+bx+c经过点A(1,0)和点B(0,5).(1)求此抛物线的解析式及顶 2020-05-16 …
如图1,已知抛物线y=-x2+bx+c经过点A(1,0)和点B(-3,0),该抛物线与y轴的交点为 2020-05-17 …
如图,已知抛物线y=-x2+2x+3与y轴交于点C,与x轴交于A,B两点,且A在B的左边,抛物线的 2020-06-14 …
有一个二次函数的题目,请各位帮帮我~~~~如图,已知抛物线的顶点为点A(3,2),且经过原点o,与 2020-06-27 …
(2009•大连)如图,抛物线F:y=ax2+bx+c的顶点为P,抛物线F与y轴交于点A,与直线O 2020-07-14 …
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点 2020-07-20 …
如图,抛物线F:y=ax^2+bx+c的顶点为P,抛物线与y轴交于点A,与直线OP交于点B,过点P 2020-07-29 …
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点 2020-07-30 …
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点 2020-07-30 …
如图是A-B-C-D-E-F是一个滑滑板的轨道截面图,其中AB,DE,EF是线段,B-C-D是一抛物 2021-01-06 …