早教吧作业答案频道 -->数学-->
已知△ABC分别以△ABC的AC,BC边为腰,A,B为直角顶点,作等腰Rt△ACE和等腰Rt△BCD,M为ED的中点,求证:AM⊥BM.
题目详情
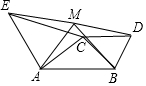
已知△ABC分别以△ABC的AC,BC边为腰,A,B为直角顶点,作等腰Rt△ACE和等腰Rt△BCD,M为ED的中点,求证:AM⊥BM.

▼优质解答
答案和解析
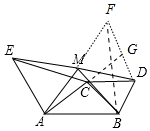
证明:延长AM至F,使MF=AM,连接DF,BF,延长AC交DF于G
∵M为ED中点,
∴MD=ME,
在△DMF和△EMA中,
,
∴△DMF≌△EMA,
∴∠MDF=∠MEA,
∴DF∥AE,
∵△ACE,△BCD 都是等腰直角三角形,
∴∠GAE=90°,∠DBC=90°,
∵DF∥AE,
∴∠DGC=∠GAE=90°,
∵∠DBC=90°,
∴在四边形DGCB中,∠BDF+∠BCG=360°-90°-90°=180°,
∵∠BCA+∠BCG=180°,
∴∠BDF=∠BCA,
∵△ACE,△BCD 都是等腰直角三角形,
∴BD=BC,AE=AC,
∵△DMF≌△EMA,
∴DF=AE,
∵AE=AC,
∴DF=AC,
在△BDF和△BCA中,
,
∴△BDF≌△BCA,
∴BF=BA,
∴△BFA是等腰三角形,
∵MF=AM,
∴BM⊥AF,
∴AM⊥BM.
∵M为ED中点,
∴MD=ME,
在△DMF和△EMA中,
|

∴△DMF≌△EMA,
∴∠MDF=∠MEA,
∴DF∥AE,
∵△ACE,△BCD 都是等腰直角三角形,
∴∠GAE=90°,∠DBC=90°,
∵DF∥AE,
∴∠DGC=∠GAE=90°,
∵∠DBC=90°,
∴在四边形DGCB中,∠BDF+∠BCG=360°-90°-90°=180°,
∵∠BCA+∠BCG=180°,
∴∠BDF=∠BCA,
∵△ACE,△BCD 都是等腰直角三角形,
∴BD=BC,AE=AC,
∵△DMF≌△EMA,
∴DF=AE,
∵AE=AC,
∴DF=AC,
在△BDF和△BCA中,
|
∴△BDF≌△BCA,
∴BF=BA,
∴△BFA是等腰三角形,
∵MF=AM,
∴BM⊥AF,
∴AM⊥BM.
看了 已知△ABC分别以△ABC的...的网友还看了以下:
在英语中,怎么样的字母叫做含有相同因素的字母.像F和D,E和B,D和M.这三组那个是含有相同因素的 2020-05-13 …
如图,在等腰△ACE中,已知CA=CE=2,AE=2c,点B、D、M分别是边AC、CE、AE的中点 2020-06-15 …
高等代数同余式约化证明过程a,b,c,d∈Z,若a≡b(modm),且d|a(d整除a),d|b, 2020-07-21 …
1stOpt能做灵敏度分析吗?y=B*(1-exp(-c*x))^m-D*(1-exp(-k*(( 2020-07-23 …
急一道数学题已知a/b=c/d=e/f=m/n(b+d+f+...+n≠0)(1)试说明:a+c+e 2020-11-01 …
matlab高手进来看看.form=1:length(l);x=0:0.01:l(m);forn=1 2020-11-04 …
设a=5,b=6,c=7,d=8,m=2,n=2,则执行表达式:(n=a>b)&&(m=c>d)设a 2020-12-15 …
已知三角形ABC和三角形DBE为等腰直角三角形,A,B,D在同一条直线上M,N,P分别是AD,AC, 2020-12-23 …
行列式X=|AB||CD|有没有简便算法(其中A,C为m阶行列行列式X=|AB||CD|有没有简便算 2020-12-24 …
指出下列集合之间的关系.A={等边三角形}B={等腰三角形}C={等腰直角三角形}D={有一个角是4 2021-01-22 …