早教吧作业答案频道 -->数学-->
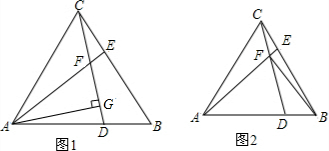
如图1,已知△ABC是等边三角形,D、E分别是AB、BC上的点,且BD=CE,AE、CD交于点F.(1)求证:△ACE≌△CBD;(2)过A作AG⊥CD于G,求证:AF=2FG;(3)如图2,若BF⊥AF,求CFAF的值.
题目详情
如图1,已知△ABC是等边三角形,D、E分别是AB、BC上的点,且BD=CE,AE、CD交于点F.
(1)求证:△ACE≌△CBD;
(2)过A作AG⊥CD于G,求证:AF=2FG;
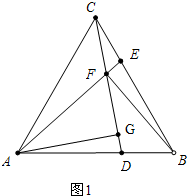
(3)如图2,若BF⊥AF,求
的值.
(1)求证:△ACE≌△CBD;
(2)过A作AG⊥CD于G,求证:AF=2FG;
(3)如图2,若BF⊥AF,求
| CF |
| AF |

▼优质解答
答案和解析
(1) 证明:如图1,∵△ABC是等边三角形,
证明:如图1,∵△ABC是等边三角形,
∴AC=BC,∠ACE=∠B=60°,
在△ACE和△CBD中,
,
∴△ACE≌△CBD
(2)∵△ACE≌△CBD,
∴∠CAE=∠BCD,
∵∠AFG=∠CAE+∠ACF=∠BCD+∠ACF=∠ACB=60°,
∵AG⊥CD,
∴∠AGF=90°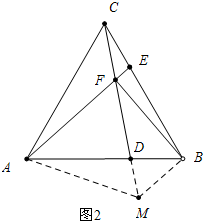
∴∠FAG=30°,
∴AF=2FG.
(3)如图2中,延长FD到M,使得∠FAM=60°,连接BM.
∵∠AFM=∠FAM=∠AMF=60°,
∴△AFM是等边三角形,
∴AF=FM=AM,
∵∠CAB=∠FAM=60°,
∴∠CAF=∠MAB,
在△CAF和△BAM中,
,
∴△CAF≌△BAM,
∴CF=BM,
∵AF⊥BF,∠AFD=60°,
∴∠MFB=30°,
∵∠AMD=∠ABC=60°,
∴AMBC四点共圆,
∴∠AMB+∠ACB=180°,
∴∠FMB=60°,
∴∠FBM=180°-∠MFB-∠FMB=90°,
∴FM=2BM,
∴AF=2CF
∴
=
.
 证明:如图1,∵△ABC是等边三角形,
证明:如图1,∵△ABC是等边三角形,∴AC=BC,∠ACE=∠B=60°,
在△ACE和△CBD中,
|
∴△ACE≌△CBD
(2)∵△ACE≌△CBD,
∴∠CAE=∠BCD,
∵∠AFG=∠CAE+∠ACF=∠BCD+∠ACF=∠ACB=60°,
∵AG⊥CD,
∴∠AGF=90°

∴∠FAG=30°,
∴AF=2FG.
(3)如图2中,延长FD到M,使得∠FAM=60°,连接BM.
∵∠AFM=∠FAM=∠AMF=60°,
∴△AFM是等边三角形,
∴AF=FM=AM,
∵∠CAB=∠FAM=60°,
∴∠CAF=∠MAB,
在△CAF和△BAM中,
|
∴△CAF≌△BAM,
∴CF=BM,
∵AF⊥BF,∠AFD=60°,
∴∠MFB=30°,
∵∠AMD=∠ABC=60°,
∴AMBC四点共圆,
∴∠AMB+∠ACB=180°,
∴∠FMB=60°,
∴∠FBM=180°-∠MFB-∠FMB=90°,
∴FM=2BM,
∴AF=2CF
∴
| CF |
| AF |
| 1 |
| 2 |
看了 如图1,已知△ABC是等边三...的网友还看了以下:
设函数fn(x)=xn+bx+c(n∈N+,b,c∈R)(1)设n≥2,b=1,c=-1,证明:设函 2020-03-30 …
(1)已知abc属于正实数,求证(a^2+a+1)(b^2+b+1)(c^2+c+1)>=27ab 2020-04-27 …
已知数列{an}:a1,a2,…,an(n≥3),令集合T={x|x=ai+aj,1≤i<j≤n} 2020-05-14 …
由a=b一定可以得出的等式是()A.a÷c=b÷c由a=b一定可以得出的等式是()A.a÷c=b÷ 2020-06-06 …
已知f(x)在[0,1]上可微,且f(0)=0,f(1)=1,求证:在(0,1)上至少有一点c,使 2020-07-07 …
已知圆C的圆心坐标原点,且过点M(1,根号3)问:(1)求圆C的方程(2)已知点P是圆C上的动点, 2020-07-26 …
已知抛物线C的顶点在原点,对称轴是y轴,抛物线上的点M(2,m)(m>0)到抛物线焦点F的距离为2 2020-07-26 …
关于三元一次方程的题1、已知x/2=y/3=z/4.,且x+y-z=1/12,求x,y,z2、已知 2020-08-03 …
1.已知xy=5,a-b=3,a+b=4,求xya的平方-xyb的平方2.因式分解(a+b+c)的平 2020-11-03 …
下列句子主干提取正确的一项是:()A、(坚持住),就(可以取得胜利).B、古往今来科学上的(新发现) 2020-11-17 …