早教吧作业答案频道 -->数学-->
已知直线AB∥CD,点P是直线AB上一动点,点E是∠ACD平分线上的点,连接PE,作∠BPE的平分线PF交CD于点F.(1)如图1,若∠PEC小于180°时,直接写出,∠ACE、∠BPF、∠PEC的数量关系;(2)如图2
题目详情
已知直线AB∥CD,点P是直线AB上一动点,点E是∠ACD平分线上的点,连接PE,作∠BPE的平分线PF交CD于点F.
(1)如图1,若∠PEC小于180°时,直接写出,∠ACE、∠BPF、∠PEC的数量关系;
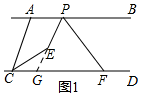
(2)如图2若点P在CE的延长线上时,求证:
∠ACE+∠BPF=90°;
(3)在(2)的条件下,分别延长CA、FP相交于点M,若∠CMF=∠APC,求:∠ACF的度数.
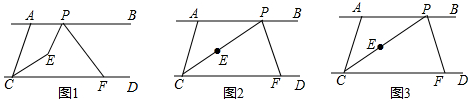
(1)如图1,若∠PEC小于180°时,直接写出,∠ACE、∠BPF、∠PEC的数量关系;
(2)如图2若点P在CE的延长线上时,求证:
| 1 |
| 2 |
(3)在(2)的条件下,分别延长CA、FP相交于点M,若∠CMF=∠APC,求:∠ACF的度数.

▼优质解答
答案和解析
 (1)∠ACE、∠BPF、∠PEC的数量关系为:∠ACE+2∠BPF=∠PEC.
(1)∠ACE、∠BPF、∠PEC的数量关系为:∠ACE+2∠BPF=∠PEC.
理由:如图1,延长PE交CD于G,
∵CE平分∠ACD,
∴∠ACE=∠ECG,
∵AB∥CD,
∴∠EGC=∠BPE,
∵PF平分∠BPE,
∴∠EGC=∠BPE=2∠BPF,
∵∠PEC是△CEG的外角,
∴∠ECG+∠EGC=∠PEC,
∴∠ACE+2∠BPF=∠PEC;
(2)如图2,∵CE平分∠ACD,PF平分∠BPE,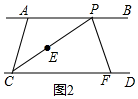
∴∠ACE=∠ECD,∠BPE=2∠BPF,
∵AB∥CD,点P在CE的延长线上,
∴∠BPE+∠ECD=180°,
∴2∠BPF+∠ACE=180°,
即
∠ACE+∠BPF=90°;
(3)如图3,∵CE平分∠ACD,PF平分∠BPE,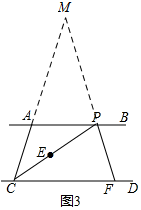
∴∠ACE=∠ECD,∠BPE=2∠EPF,
∵AB∥CD,
∴∠ECD=∠APC,
又∵∠CMF=∠APC,
∴∠ECD=∠CMF,
设∠ACE=∠ECD=α,则∠CMF=α,∠ACF=2α,
∵∠CPF是△PCM的外角,
∴∠EPF=∠M+∠ACP=2α,
∴∠BPE=2∠EPF=4α,
∵AB∥CD,点P在CE的延长线上,
∴∠BPE+∠ECD=180°,
即4α+α=180°,
∴α=36°,
∴∠ACF=2α=72°.
 (1)∠ACE、∠BPF、∠PEC的数量关系为:∠ACE+2∠BPF=∠PEC.
(1)∠ACE、∠BPF、∠PEC的数量关系为:∠ACE+2∠BPF=∠PEC.理由:如图1,延长PE交CD于G,
∵CE平分∠ACD,
∴∠ACE=∠ECG,
∵AB∥CD,
∴∠EGC=∠BPE,
∵PF平分∠BPE,
∴∠EGC=∠BPE=2∠BPF,
∵∠PEC是△CEG的外角,
∴∠ECG+∠EGC=∠PEC,
∴∠ACE+2∠BPF=∠PEC;
(2)如图2,∵CE平分∠ACD,PF平分∠BPE,

∴∠ACE=∠ECD,∠BPE=2∠BPF,
∵AB∥CD,点P在CE的延长线上,
∴∠BPE+∠ECD=180°,
∴2∠BPF+∠ACE=180°,
即
| 1 |
| 2 |
(3)如图3,∵CE平分∠ACD,PF平分∠BPE,

∴∠ACE=∠ECD,∠BPE=2∠EPF,
∵AB∥CD,
∴∠ECD=∠APC,
又∵∠CMF=∠APC,
∴∠ECD=∠CMF,
设∠ACE=∠ECD=α,则∠CMF=α,∠ACF=2α,
∵∠CPF是△PCM的外角,
∴∠EPF=∠M+∠ACP=2α,
∴∠BPE=2∠EPF=4α,
∵AB∥CD,点P在CE的延长线上,
∴∠BPE+∠ECD=180°,
即4α+α=180°,
∴α=36°,
∴∠ACF=2α=72°.
看了 已知直线AB∥CD,点P是直...的网友还看了以下:
数轴上点A对应的数是-1,B点对应的数是1,点A、B、C分别以1单位一秒,三单位一秒,四单位一秒在数 2020-03-30 …
数轴上点A对应的数是-1,B点对应的数是1,点A、B、C分别以1单位一秒,三单位一秒,四单位一秒在数 2020-03-30 …
全站仪知道2个点的坐标求第3点坐标3个点在一条直线上点A:538.148548.223点B:544 2020-04-07 …
已知边长为4的等边三角形ABC,顶点B在坐标原点,顶点C在X轴正半轴上,顶点A在X轴上方.现将△A 2020-05-16 …
1、点(a、b)关于Y轴的对称点的坐标是()A.(-a,-b)B.(a,-b)C.(-a,b)D. 2020-05-22 …
已知ABC中,点A,B的坐标分别为(-√2,0)(√2,0)点C在X轴上方若点C坐标(√2,1), 2020-06-21 …
阅读理若A、B、C为数轴上三点且点C在点A、点B之间,若点C到A的距离是点C到B的距离2倍,我们就 2020-07-14 …
如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,如果|a|>|c|>|b|,那 2020-07-30 …
阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是A,B的好 2020-07-30 …
阅读理若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是A,B的妙点. 2020-07-30 …