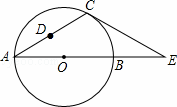
如图，在△ACE中，CA=CE，∠CAE=30°，⊙O经过点C，且圆的直径AB在线段AE上．（1）试说明CE是⊙O的切线；（2）若△ACE中AE边上的高为h，试用含h的代

Question

如图，在 △ACE 中， CA=CE ， ∠CAE=30° ， ⊙O 经过点 C ，且圆的直径 AB 在线段 AE 上．

（ 1 ）试说明 CE 是 ⊙O 的切线；

（ 2 ）若 △ACE 中 AE 边上的高为 h ，试用含 h 的代数式表示 ⊙O 的直径 AB ；

（ 3 ）设点 D 是线段 AC 上任意一点（不含端点），连接 OD ，当 CD+OD 的最小值为 6 时，求 ⊙O 的直径 AB 的长．

Answer 1

（ 1 ）连接 OC ，如图 1 ，

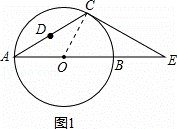
∵CA=CE ， ∠CAE=30° ，

∴∠E=∠CAE=30° ， ∠COE=2∠A=60° ，

∴∠OCE=90° ，

∴CE 是 ⊙O 的切线；

（ 2 ）过点 C 作 CH⊥AB 于 H ，连接 OC ，如图 2 ，

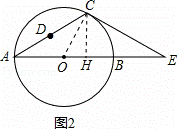
由题可得 CH=h ．

在 Rt△OHC 中， CH=OC•sin∠COH ，

∴h=OC•sin60°= OC ，

∴OC= = h ，

∴AB=2OC= h ；

（ 3 ）作 OF 平分 ∠AOC ，交 ⊙O 于 F ，连接 AF 、 CF 、 DF ，如图 3 ，

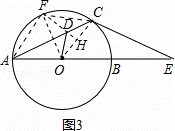
则 ∠AOF=∠COF= ∠AOC= （ 180° ﹣ 60° ） =60° ．

∵OA=OF=OC ，

∴△AOF 、 △COF 是等边三角形，

∴AF=AO=OC=FC ，

∴ 四边形 AOCF 是菱形，

∴ 根据对称性可得 DF=DO ．

过点 D 作 DH⊥OC 于 H ，

∵OA=OC ， ∴∠OCA=∠OAC=30° ，

∴DH=DC•sin∠DCH=DC•sin30°= DC ，

∴ CD+OD=DH+F D ．

根据两点之间线段最短可得：

当 F 、 D 、 H 三点共线时， DH+FD （即 CD+OD ）最小，

此时 FH=OF•sin∠FOH= OF=6 ，

则 OF=4 ， AB=2OF=8 ．

∴ 当 CD+OD 的最小值为 6 时， ⊙O 的直径 AB 的长为 8 ．