在正方形ABCD中，AB=4，动点E在AB上（0＜EA＜2），现将正方形沿着过E点的直线翻折，使得点B落在边AD上的点F，翻折后边BC所在的直线与DC交于G．（1）求证：△EAF∽△FDG；（2）试探究：

Question

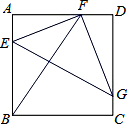在正方形ABCD中，AB=4，动点E在AB上（0＜EA＜2），现将正方形沿着过E点的直线翻折，使得点B落在边AD上的点F，翻折后边BC所在的直线与DC交于G．
（1）求证：△EAF∽△FDG；
（2）试探究：在点E运动的过程中，△FDG的周长是否发生变化？若变化，请说明理由；若不变化，求出它的值．

Answer 1

考点：
相似三角形的判定与性质 正方形的性质 翻折变换（折叠问题）
专题：

分析：
（1）易证∠DFG=∠AEF，即可证明△EAF∽△FDG；（2）不变；理由：设BE=x，FA=y，根据勾股定理可得EF2=AE2+AF2，即可求得y2=-64+16x，根据△EAF∽△FDG可得FDAE=C△DFGC△AEF，即可求得C△DFG=64-y28-x，即可解题．

证明：（1）∵∠EFA+∠AEF=90°，∠EFA+∠DFG=90°，∴∠DFG=∠AEF，∵∠A=∠D=90°，∴△EAF∽△FDG；（2）不变；理由：设BE=x，FA=y，在RT△AEF中，EF2=AE2+AF2，∴x2=（8-x）2+y2，∴y2=-64+16x，∵△EAF∽△FDG，∴FDAE=C△DFGC△AEF，∴8-y8-x=C△DFG8+y，∴C△DFG=64-y28-x=16，∴△FDG的周长不变．
点评：
本题考查了相似三角形的判定，考查了相似三角形对应边比例等于周长比的性质，本题中求证△EAF∽△FDG是解题的关键．