早教吧作业答案频道 -->数学-->
如图所示,P、Q分别是Rt△ABC两直角边AB、AC上两点,M为斜边BC的中点,且PM⊥QM,MD⊥AB于点D,ME⊥AC于点E.求证:(1)△MPD∽△MQE;(2)AD•PD=AE•EQ:(3)PB2+QC2=PM2+QM2.
题目详情
如图所示,P、Q分别是Rt△ABC两直角边AB、AC上两点,M为斜边BC的中点,且PM⊥QM,MD⊥AB于点D,ME⊥AC于点E.求证:
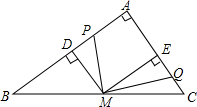
(1)△MPD∽△MQE;
(2)AD•PD=AE•EQ:
(3)PB2+QC2=PM2+QM2.

(1)△MPD∽△MQE;
(2)AD•PD=AE•EQ:
(3)PB2+QC2=PM2+QM2.
▼优质解答
答案和解析
证明:(1)∵MD⊥AB于点D,ME⊥AC,∠A=90°,
∴∠MDP=∠MEA=∠A=90°,
∴四边形ADME是矩形,
∴AD=EM,AE=DM,∠DME=90°,
∵PM⊥QM,
∴∠PMQ=90°,
∴∠DMP=∠EMQ,
∴△MPD∽△MQE;
(2)∵△MPD∽△MQE,
∴
=
,
∵AD=EM,AE=DM,
∴
=
,
∴AD•PD=AE•EQ;
(3)如图,以M点为中心,△MCQ顺时针旋转180°至△MBN,
∴△MCQ≌△MBN,
∴BN=QC,MN=MQ,∠MBN=∠C,
连接PN,PQ,
∵PM⊥QM,
∴PM垂直平分NQ,
∴PN=PQ,
∵△ABC是直角三角形,BC是斜边,
∴∠ABC+∠C=90°,
∴∠ABC+∠MBN=90°,
即△PBN是直角三角形,
根据勾股定理可得,PN2=PB2+BN2,
∴PQ2=PB2+QC2,
∵PQ2=PM2+QM2,
∴PB2+QC2=PM2+QM2.
∴∠MDP=∠MEA=∠A=90°,
∴四边形ADME是矩形,
∴AD=EM,AE=DM,∠DME=90°,
∵PM⊥QM,
∴∠PMQ=90°,
∴∠DMP=∠EMQ,
∴△MPD∽△MQE;
(2)∵△MPD∽△MQE,
∴
| PD |
| EQ |
| DM |
| EM |

∵AD=EM,AE=DM,
∴
| PD |
| EQ |
| AE |
| AD |
∴AD•PD=AE•EQ;
(3)如图,以M点为中心,△MCQ顺时针旋转180°至△MBN,
∴△MCQ≌△MBN,
∴BN=QC,MN=MQ,∠MBN=∠C,
连接PN,PQ,
∵PM⊥QM,
∴PM垂直平分NQ,
∴PN=PQ,
∵△ABC是直角三角形,BC是斜边,
∴∠ABC+∠C=90°,
∴∠ABC+∠MBN=90°,
即△PBN是直角三角形,
根据勾股定理可得,PN2=PB2+BN2,
∴PQ2=PB2+QC2,
∵PQ2=PM2+QM2,
∴PB2+QC2=PM2+QM2.
看了 如图所示,P、Q分别是Rt△...的网友还看了以下:
下列各项中注音有误的一项是()A.嬖爱bì劈风斩浪pī癖好pìB.躲避bì巨擘bò复辟bì开辟pì 2020-05-13 …
在括号内填写理由.如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.证明:∵∠ 2020-05-16 …
设实数a,b,c,d,e满足(a+c)(a+d)=(b+c)(b+d)=e≠O,且a≠b,那么(a 2020-06-08 …
设A为n(n≥2)阶可逆矩阵,交换A的第1行与第2行得矩阵B,A*,B*分别为A,B的伴随矩阵,则 2020-07-22 …
已知α-l-β是大小确定的一个二面角,若a,b是空间两条直线,则能使a,b所成的角为定值的一个条件是 2020-11-02 …
设α,β,γ是平面,a,b是直线,则以下结论正确的是()A.若a∥b,a⊂α,则b∥αB.若α⊥β, 2020-11-02 …
若直线a⊥直线b,且a⊥平面α,则有()A.b∥αB.b⊂αC.b⊥αD.b∥α或b⊂α 2020-11-02 …
下列词语中加点的字,读音全都正确的一组是A.装载(zǎi)骤然(zhòu)摇曳(yì)跌宕(dàng 2020-11-06 …
下列加点字的读音正确的一项是A.趴在地上pā含情脉脉mò差劲chà好恶wùB.钥匙yuè度命dù差遣 2020-12-19 …
若a,b是有理数,那么下列结论一定正确的是()A.若a<b,则|a|<|b|B.若a>b,则|a|> 2020-12-23 …