早教吧作业答案频道 -->数学-->
如图,在长方形ABCO中,点B(8,6),(1)点M在边AB上,若△OCM是等腰三角形,试求M的坐标;(2)点P是线段BC上一动点,0≤PC≤6.已知点D在第一象限,是直线y=2x-6上的一点,若△ADP是等腰
题目详情
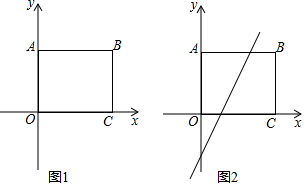
如图,在长方形ABCO中,点B(8,6),
(1)点M在边AB上,若△OCM是等腰三角形,试求M的坐标;
(2)点P是线段BC上一动点,0≤PC≤6.已知点D在第一象限,是直线y=2x-6上的一点,若△ADP是等腰三角形,且∠ADP=90°,请求出点D的坐标.
(1)点M在边AB上,若△OCM是等腰三角形,试求M的坐标;
(2)点P是线段BC上一动点,0≤PC≤6.已知点D在第一象限,是直线y=2x-6上的一点,若△ADP是等腰三角形,且∠ADP=90°,请求出点D的坐标.

▼优质解答
答案和解析
 (1)分三种情况:
(1)分三种情况:
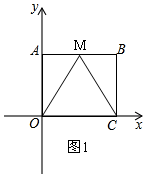
①当OM=MC时,如图1,
∵四边形ABCO是长方形,
∴∠OAM=∠B=90°,AO=BC,
∴Rt△AOM≌Rt△BCM,
∴AM=BM,
∵B(8,6),
∴M(4,6);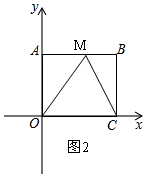
②当OM=OC时,如图2,
∵OC=8,
∴OM=8,
在Rt△OAM中,由勾股定理得:AM=
=2
,
∴M(2
,6),
③当OC=CM时,同理得:BM=2
,
∴AM=8-2
,
∴M(8-2
,6),
综上所述,点M的坐标为:(4,6)或(2
,6)或(8-2
,6);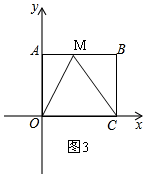
(2)分两种情况:
①当D在长方形ABCO内部时,如图4,P与B重合,
∵∠ADP=90°,△ADP是等腰三角形,
∴△ADP是等腰直角三角形,
过D作DE⊥AB于E,
∴AE=ED=BE=4,
∴D(4,2),
②当D在长方形ABCO外部时,如图5,∠ADP=90°,AD=PD,
过D作EF∥AB,交y轴于E,交CB延长线于F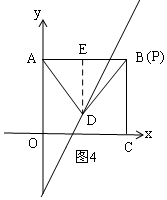 ,
,
∴∠AED=∠DFP=90°,
∴∠EAD+∠EDA=90°,
∵∠ADP=90°,
∴∠EDA+∠PDF=90°,
∴∠EAD=∠PDF,
∵AD=PD,
∴△ADE≌△DFP,
∴AE=DF,
设D(m,2m-6),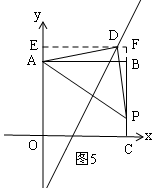
∴2m-6-6=8-m,
m=
,
∴2m-6=
,
∴D(
,
),
综上所述,点D的坐标为(4,2)或(
 (1)分三种情况:
(1)分三种情况:①当OM=MC时,如图1,
∵四边形ABCO是长方形,
∴∠OAM=∠B=90°,AO=BC,
∴Rt△AOM≌Rt△BCM,
∴AM=BM,
∵B(8,6),
∴M(4,6);

②当OM=OC时,如图2,
∵OC=8,
∴OM=8,
在Rt△OAM中,由勾股定理得:AM=
| 82-62 |
| 7 |
∴M(2
| 7 |
③当OC=CM时,同理得:BM=2
| 7 |
∴AM=8-2
| 7 |
∴M(8-2
| 7 |
综上所述,点M的坐标为:(4,6)或(2
| 7 |
| 7 |

(2)分两种情况:
①当D在长方形ABCO内部时,如图4,P与B重合,
∵∠ADP=90°,△ADP是等腰三角形,
∴△ADP是等腰直角三角形,
过D作DE⊥AB于E,
∴AE=ED=BE=4,
∴D(4,2),
②当D在长方形ABCO外部时,如图5,∠ADP=90°,AD=PD,
过D作EF∥AB,交y轴于E,交CB延长线于F
 ,
,∴∠AED=∠DFP=90°,
∴∠EAD+∠EDA=90°,
∵∠ADP=90°,
∴∠EDA+∠PDF=90°,
∴∠EAD=∠PDF,
∵AD=PD,
∴△ADE≌△DFP,
∴AE=DF,
设D(m,2m-6),

∴2m-6-6=8-m,
m=
| 20 |
| 3 |
∴2m-6=
| 22 |
| 3 |
∴D(
| 20 |
| 3 |
| 22 |
| 3 |
综上所述,点D的坐标为(4,2)或(
看了 如图,在长方形ABCO中,点...的网友还看了以下:
1.已知:P={0,1},M={x/x包含于P},则P与M的关系为A.P∈M B.P不属于M C. 2020-05-13 …
>symsna0b0c0;>>M=sym('[1,1/2,0;0,1/2,1;0,0,0]');> 2020-05-17 …
平面向量.的问题已知P={a|a=(1,0)+m(0,1),m∈R},Q={b|b=(1,1)+n 2020-06-06 …
高分求一道初三二次根式题!已知:实数m、n、p满足m+n+|√(p-1)-1|=4√m-2+2√n 2020-06-06 …
已知m,n,p,q满足:mnpq=6(m-1)(n-1)(p-1)(q-1).(1).若m,n,p 2020-06-11 …
若集合M={x丨-3≤x≤4},集合P={x丨2m-1≤x≤m+1}.(1)证明:M与P不可能相等 2020-06-12 …
设M、N为两个随机事件,给出以下命题:(1)若M、N为互斥事件,且P(M)=15,P(N)=14, 2020-07-09 …
已知P(2m-5,m-1)当m为何值时(1)P在二,四象限角平分线上?(2)P在一,三象限角平已知 2020-07-16 …
几何分布无记忆性证明中证:P{x=m+n|x>m}=P(X=m+n,x>m)/P{x>m}=P(X= 2020-10-31 …
X、Y分别服从参数为(n,p)(m,p)的二项分布,通过计算求出X+Y的分布我用的方法Z=X+YP( 2020-10-31 …
 扫描下载二维码
扫描下载二维码
