早教吧作业答案频道 -->数学-->
抛物线y=ax2+c与x轴交于A,B两点,顶点C,点P为抛物线上一点,且位于x轴下方.(1)如图1,若P(1,-3),B(4,0).D是抛物线上一点,满足∠DPO=∠POB,且D与B分布位于直线OP的两侧,求点C
题目详情
抛物线y=ax2+c与x轴交于A,B两点,顶点C,点P为抛物线上一点,且位于x轴下方.
(1)如图1,若P(1,-3),B(4,0).D是抛物线上一点,满足∠DPO=∠POB,且D与B分布位于直线OP的两侧,求点C与点D的坐标;
(2)如图2,A,B是抛物线y=ax2+c与x轴的两个交点,直线PA,PB与y轴分别交于E,F两点,当点P在x轴下方的抛物线上运动时,
是否为定值?若是,试求出该定值;若不是,请说明理由(记OA=OB=t)
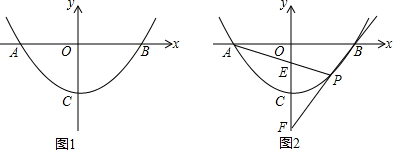
(1)如图1,若P(1,-3),B(4,0).D是抛物线上一点,满足∠DPO=∠POB,且D与B分布位于直线OP的两侧,求点C与点D的坐标;
(2)如图2,A,B是抛物线y=ax2+c与x轴的两个交点,直线PA,PB与y轴分别交于E,F两点,当点P在x轴下方的抛物线上运动时,
| OE+OF |
| OC |

▼优质解答
答案和解析
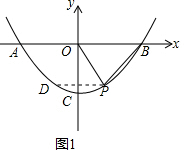 (1)将P(1,-3),B(4,0)代入y=ax2+c,得
(1)将P(1,-3),B(4,0)代入y=ax2+c,得
,
解得
,
抛物线的解析式为y=
x2-
.
∴C(0,-
)
如图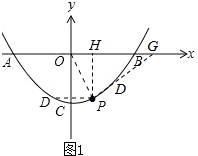 1,
1,
当点D在OP左侧时,
由∠DPO=∠POB,得
DP∥OB,
D与P关于y轴对称,P(1,-3),
得D(-1,-3);
(2)点P运动时,
是定值,定值为2,理由如下: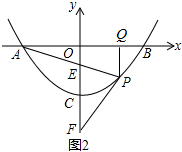
作PQ⊥AB于Q点,设P(m,am2+c),A(-t,0),B(t,0),则at2+c=0,c=-at2.
∵PQ∥OF,
∴
=
,
∴OF=
=-
=
=amt+at2.
同理OE=-amt+at2.
∴OE+OF=2at2=-2c=2OC.
∴
=2.
 (1)将P(1,-3),B(4,0)代入y=ax2+c,得
(1)将P(1,-3),B(4,0)代入y=ax2+c,得
|
解得
|
抛物线的解析式为y=
| 1 |
| 5 |
| 16 |
| 5 |
∴C(0,-
| 16 |
| 5 |
如图
 1,
1,当点D在OP左侧时,
由∠DPO=∠POB,得
DP∥OB,
D与P关于y轴对称,P(1,-3),
得D(-1,-3);
(2)点P运动时,
| OE+OF |
| OC |

作PQ⊥AB于Q点,设P(m,am2+c),A(-t,0),B(t,0),则at2+c=0,c=-at2.
∵PQ∥OF,
∴
| PQ |
| OF |
| BQ |
| BO |
∴OF=
| PQ•BO |
| BQ |
| -(am2+c)t |
| t-m |
| (am2-at2)t |
| m-t |
同理OE=-amt+at2.
∴OE+OF=2at2=-2c=2OC.
∴
| OE+OF |
| OC |
看了 抛物线y=ax2+c与x轴交...的网友还看了以下:
若X^2a+b-2X^a-b+3=o是关于X的一元二次方程,求a、b的值.张敏是这样考虑的:满足条 2020-04-26 …
若X^2a+b-2X^a-b+3=o是关于X的一元二次方程,求a、b的值.张敏是这样考虑的:满足条 2020-04-26 …
已知异面直线a,b的公垂线段AB的中点为O,平面α满足a∥α,b∥α,且O∈α,M、N是a,b上的 2020-06-27 …
已知A是三阶矩阵,B是三阶矩阵,求满足BA=O的所有B?满足AB=O,我知道是求Ax=0的通解;反 2020-07-19 …
过△ABC所在平面外一点P,作PO⊥,垂足为O,连接PA、PB、PC且PA、PB、PC两两垂直,则 2020-07-30 …
如图,有点O,O'和三角形ABC三角形A'B'C',满足下列条件:向量OA=a向量,向量OB=b向 2020-08-01 …
设n阶方阵A,B满足AB=O,其中O为零矩阵,则必有A.A=O或B=OB.︳A︳=0或︳B︳=0C. 2020-11-02 …
=1(a>b>0)的左、右焦点,过点E垂直于椭圆长轴的直线交椭圆于A、B两点,△ABF是正三角形.( 2020-11-03 …
下列画线字的注音全对的一组是A.创(chuāng)伤撇(piē)下模棱(léng)两可削(xiāo) 2020-11-16 …
下列字的注音全对的一组是A.创(chuāng)伤撇(piē)下模棱(léng)两可削(xiāo)足适 2020-12-18 …