如图，在平面直角坐标系xOy中，抛物线y=ax2+1经过点A（4，-3），顶点为点B，点P为抛物线上的一个动点，l是过点（0，2）且垂直于y轴的直线，过P作PH⊥l，垂足为H，连接PO．（1）求抛物线的

Question

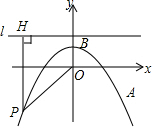
如图，在平面直角坐标系xOy中，抛物线y=ax²+1经过点A（4，-3），顶点为点B，点P为抛物线上的一个动点，l是过点（0，2）且垂直于y轴的直线，过P作PH⊥l，垂足为H，连接PO．

（1）求抛物线的解析式，并写出其顶点B的坐标；
（2）①当P点运动到A点处时，计算：PO=___，PH=___，由此发现，PO___PH（填“>”、“<”或“=”）；
②当P点在抛物线上运动时，猜想PO与PH有什么数量关系，并证明你的猜想．

Answer 1

（1） ∵抛物线y=ax²+1经过点A（4，-3），
∴-3=16a+1，
∴a=-(1)/(4)，
∴抛物线解析式为y=-(1)/(4)x²+1，顶点B（0，1）．

（2）①当P点运动到A点处时，∵PO=√(32+42)=5，PH=2-（-3）=5，
∴PO=PH，
故答案分别为5，5，=．

②结论：PO=PH．
理由：设点P坐标（m，-(1)/(4)m²+1），
∵PH=2-（-(1)/(4)m²+1）=(1)/(4)m²+1
PO=√(m2+(-(1)/(4)m2+1)2)=√(((1)/(4)m2+1)2)=(1)/(4)m²+1，
∴PO=PH．