早教吧作业答案频道 -->数学-->
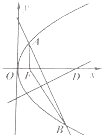
抛物线y2=4x的焦点为F,过点(0,3)的直线与抛物线交于A,B两点,线段AB的垂直平分线交x轴于点D,若|AF|+|BF|=6,则点D的横坐标为.
题目详情
抛物线y2=4x的焦点为F,过点(0,3)的直线与抛物线交于A,B两点,线段AB的垂直平分线交x轴于点D,若|AF|+|BF|=6,则点D的横坐标为___.

▼优质解答
答案和解析
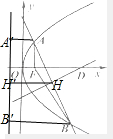 设AB的中点为H,
设AB的中点为H,
抛物线y2=4x的焦点为F(1,0),准线为x=-1,
设A,B,H在准线上的射影分别为A',B',H',
则|HH'|=
(|AA'|+|BB'|),
由抛物线的定义可得,
|AF|=|AA'|,|BF|=|BB'|,
|AF|+|BF|=6,即为|AA'|+|BB'|=6,
|HH'|=
×6=3,
即有H的横坐标为2,
设直线AB:y=kx+3,
代入抛物线方程,可得k2x2+(6k-4)x+9=0,
即有判别式(6k-4)2-36k2>0,解得k<
且k≠0,
又x1+x2=
=4,
解得k=-2或
(舍去),
则直线AB:y=-2x+3,
AB的中点为(2,-1),
AB的中垂线方程为y+1=
(x-2),
令y=0,解得x=4,
则D(4,0).
故答案为:4.
 设AB的中点为H,
设AB的中点为H,抛物线y2=4x的焦点为F(1,0),准线为x=-1,
设A,B,H在准线上的射影分别为A',B',H',
则|HH'|=
| 1 |
| 2 |
由抛物线的定义可得,
|AF|=|AA'|,|BF|=|BB'|,
|AF|+|BF|=6,即为|AA'|+|BB'|=6,
|HH'|=
| 1 |
| 2 |
即有H的横坐标为2,
设直线AB:y=kx+3,
代入抛物线方程,可得k2x2+(6k-4)x+9=0,
即有判别式(6k-4)2-36k2>0,解得k<
| 1 |
| 3 |
又x1+x2=
| 4-6k |
| k2 |
解得k=-2或
| 1 |
| 2 |
则直线AB:y=-2x+3,
AB的中点为(2,-1),
AB的中垂线方程为y+1=
| 1 |
| 2 |
令y=0,解得x=4,
则D(4,0).
故答案为:4.
看了 抛物线y2=4x的焦点为F,...的网友还看了以下:
在平面直角坐标系中,已知焦距为4的椭圆C:x^2/a^2+y^2/b^2=1(a>b>0)的右焦点 2020-05-15 …
1.直线y=kx+b与x轴交点的横坐标,是一元一次方程的解?如直线y=-x+1与x轴交点横坐标即x 2020-05-19 …
直角坐标系集合问题直角坐标系中坐标轴上的点的集合可表示为:A.{(x,y)|x=0,y≠0或x≠0 2020-06-03 …
如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B。P为线段AB上一动 2020-06-08 …
如图直线y=2x+6分别与x轴、y轴相交于A、C两点(求出后A坐标为(-3,0)C坐标为(0,6) 2020-06-13 …
若A={(x,y)|(x-1)^2+(y-2)^2≤5/4}与B={(x,y)||x-1|+2|y 2020-06-14 …
在平面直角坐标系中,点P(a,b)到直线x=2的距离为3,则a的值若x轴的点p到y轴的距离为3,则 2020-06-14 …
在平面直角坐标系中,一次函数y=Kx+b(b小于0)的图像分别与x轴、y轴和直线x=4交于A、B、 2020-06-14 …
在平面直角坐标系中,直线L1与x轴、y轴分别交于C、D两点,且直线上所有点的坐标(x,y)均是二元一 2020-11-01 …
立体坐标系指定距离坐标公式立体坐标系(x,y,z)中已知A(Xa,Ya,Zz),B(Xb,Yb,Zb 2020-12-25 …